Giải Bài tập 8 trang 81 sgk Toán 8 tập 1 Chân trời

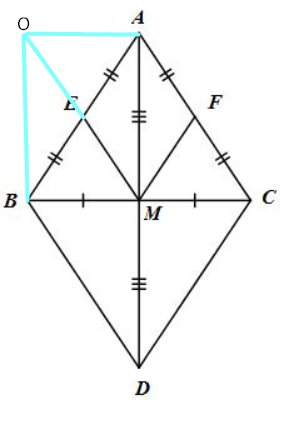
a) Tứ giác ABCD có:

AD và BC cắt nhau tại M (gt);

M là trung điểm của BC (gt)

M là trung điểm của AD (D đối xứng với A qua BC)

Do đó tứ giác ABDC là hình bình hành

Mà AD⊥BC (vì D đối xứng với A qua BC)

Nên hình bình hành ABDC là hình thoi.

b) Tứ giác OAMB có:

OM và AB cắt nhau tại E (gt);

E là trung điểm của OM (gt)

E là trung điểm của AB (gt)

Do đó tứ giác OAMB là hình bình hành

Suy ra $\widehat{AOB}=\widehat{AMB}=90^{\circ},\widehat{OBM}=\widehat{OAM}=180^{\circ}-90^{\circ}=90^{\circ}$ 

Do đó AOB và MBO là tam giác vuông.

Xét tam giác AOB và MBO ta có:

AO = MB (OAMB là hình bình hành)

$\widehat{AOB}=\widehat{MBO}=90^{\circ}$

OB chung

Suy ra $\Delta AOB=\Delta MBO$ (c.g.c)

c) Ta có ME=$\frac{1}{2}AB$ (đường trung tuyến ứng với cạnh huyền)

Và AE=$\frac{1}{2}AB$ (E là trung điểm của AB)

⇒EM=EA=$\frac{1}{2}AB$ (1)

Ta có MF=$\frac{1}{2}AC$ (đường trung tuyến ứng với cạnh huyền)

Và AF=$\frac{1}{2}AC$ (F là trung điểm của AC)

⇒MF=AF=$\frac{1}{2}$AC(2)

AB=AC(ΔABCcân tại A)  (3)

Từ (1), (2) và (3) suy ra EM = EA = MF = AF

Do đó tứ giác AEMF là hình thoi.