Giải Bài tập 5 trang 80 sgk Toán 8 tập 1 Chân trời
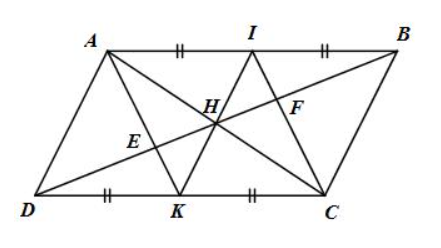
Bài tập 5 trang 80 sgk Toán 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, E và F là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AKCI là hình bình hành.
b) Chứng minh rằng DE = EF = FB.
a) Ta có:
AI=$\frac{1}{2}AB$ (I là trung điểm của AB),
CK=$\frac{1}{2}CD$ (K là trung điểm của CD)
Và AB=CD(ABCD là hình bình hành)
⇒AI=CK
Mà AI // CK (AB//CD,I∈AB,K∈CD)
Do đó tứ giác AICK là hình bình hành.
b) ΔABEcó I là trung điểm của AB và IF//AE
Nên F là trung điểm của EB ⇒BF=EF (1)
ΔDCFcó EK // FC và K là trung điểm của CD
Nên E là trung điểm của DF ⇒DE=EF (2)
Từ (1) và (2) suy ra DE=EF=BF

Bình luận