Giải bài tập 4.37 trang 66 SBT toán 10 tập 1 kết nối

Trả lời:

a) Có $\overrightarrow{AB}$ = (4; 3), $\overrightarrow{AC}$ = (6; -3)

$\Rightarrow \overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương

$\Rightarrow$ ba điểm A, B, C không thẳng hàng

$\Rightarrow$ ba điểm A, B, C là một tam giác

Gọi G là trọng tâm của tam giác ABC

$\Rightarrow$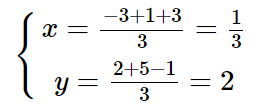  

Vậy điểm $G(\frac{1}{3}; 2)$

b) Gọi $H(x_{H}; y_{H})$ là trực tâm của tam giác ABC ta có

$\overrightarrow{BH}$ = $(x_{H} - 1; y_{H} - 5)$, $\overrightarrow{CH}$ = $(x_{H} - 3; y_{H} + 1)$

Lại có BH $\perp$ AC, CH $\perp$ AB

Nên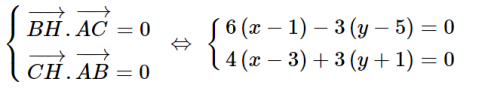  

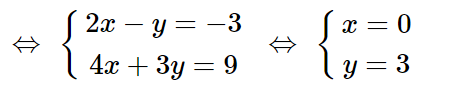
Vậy H(0; 3)

c) Gọi $I(x_{I}; y_{I})$ là tâm đường tròn ngoại tiếp tam giác BAC ta có

$\overrightarrow{IH} = 3\overrightarrow{IG}$

$\Leftrightarrow (-x_{I}; 3 - y_{I}) = 3(\frac{1}{3} - x_{I}; 6 - 3y_{I})$

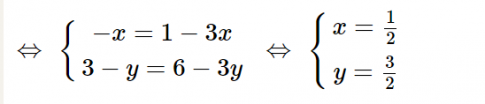
Vậy $I(\frac{1}{2}; (\frac{3}{2})$