Giải bài tập 4.29 trang 69 SBT toán 10 tập 1 kết nối

Trả lời:

a) 

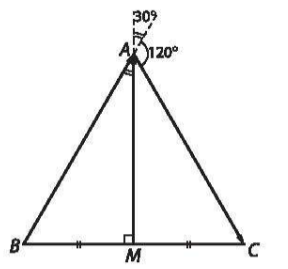
Do tam giác ABC là tam giác đều với độ dài các cạnh bằng 1

Lại có M là trung điểm BC suy ra MA = $\frac{\sqrt{3}}{2}$

($\overrightarrow{MA}$; $\overrightarrow{BA}$) = $30^{o}$, ($\overrightarrow{MA}$; $\overrightarrow{AC}$) = 120^{o}$

Suy ra $\overrightarrow{MA}$ . $\overrightarrow{BA}$ = |$\overrightarrow{MA}$| . |$\overrightarrow{BA}$| .cos($\overrightarrow{MA}$; $\overrightarrow{BA}$) = $\frac{3}{2}$

$\overrightarrow{MA}$ . $\overrightarrow{AC}$ = |$\overrightarrow{MA}$| . |$\overrightarrow{AC}$| .cos($\overrightarrow{MA}$; $\overrightarrow{AC}$) =  $\frac{-\sqrt{3}}{4}$

b) 

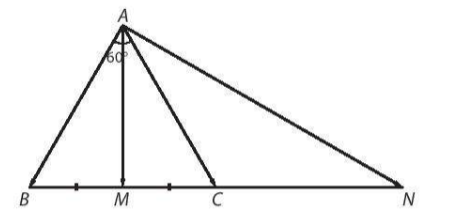
Do tam giác ABC đều nên ($\overrightarrow{AB}$; $\overrightarrow{AC}$) = $60^{o}$ (1)

M là trung điểm của BC nên $\overrightarrow{AM} =  \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$ (2)

N đối xứng với B qua C nên C là trung điềm của BN suy ra $\overrightarrow{AN} = 2\overrightarrow{AC} - \overrightarrow{AB}$ (3)

Từ (1), (2) và (3) suy ra  $\overrightarrow{AM} . \overrightarrow{AN} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) . (2\overrightarrow{AC} - \overrightarrow{AB})$

$\overrightarrow{AM} . \overrightarrow{AN} = \frac{1}{2}(\overrightarrow{AB}.\overrightarrow{AC} + 2\overrightarrow{MA}^{2} - \overrightarrow{AB}^{2})$

$\overrightarrow{AM} . \overrightarrow{AN} = \frac{3}{4}$

c)

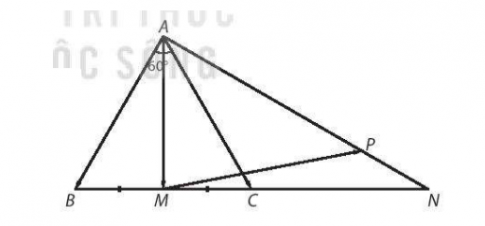
P thuộc đoạn AN thỏa mãn AP = 3AN nên $\overrightarrow{AP} = \frac{3}{4}\overrightarrow{AN} = \frac{3}{2}\overrightarrow{AC} - \frac{3}{4}\overrightarrow{AB}$ 

Suy ra $\overrightarrow{MP} = \overrightarrow{AP} - \overrightarrow{AM} = (\frac{3}{2}\overrightarrow{AC} - \frac{3}{4}\overrightarrow{AB}) - (\frac{1}{2}\overrightarrow{AB} + \overrightarrow{AC}) = \overrightarrow{AC} - \frac{5}{4}\overrightarrow{AB}$

Từ đó ta có $MP^{2} = \overrightarrow{MP}^{2} = (\overrightarrow{AC} - \frac{5}{4}\overrightarrow{AB})^{2}$

$MP^{2} = \overrightarrow{AC}^{2} + \frac{25}{16}\overrightarrow{AB}^{2} - 2.\overrightarrow{AC}.\frac{5}{4}\overrightarrow{AB}$

$MP^{2} = 1 +  \frac{25}{16} -  \frac{5}{2} . 1 . 1.  \frac{1}{2} =  \frac{21}{16}$

Vậy MP = $\frac{\sqrt{21}}{4}$