Giải bài tập 4.30 trang 69 SBT toán 10 tập 1 kết nối
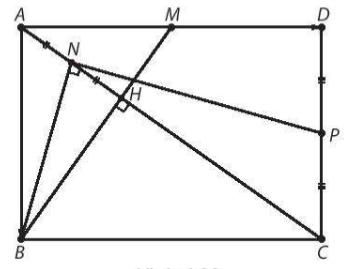
Bài tập 4.30. Cho hình chữ nhật ABCD có AB = 1, BC = $\sqrt{2}$. Gọi M là trung điểm của AD.
a) Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.
b) Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằng tam giác NBP là một tam giác vuông.
Trả lời:
a) Đặt $\overrightarrow{AB} = \overrightarrow{b}$ $\overrightarrow{AD} = \overrightarrow{d}$ với |$\overrightarrow{b}$| = 1, |$\overrightarrow{d}$| = $\sqrt{2}$ và $\overrightarrow{b} . \overrightarrow{d} = 0$
Khi đó $\overrightarrow{AC} = \overrightarrow{b} + \overrightarrow{d}$
M là trung điểm AD nên $\overrightarrow{AM} = \frac{1}{2}\overrightarrow{d}$ và $\overrightarrow{BM} = \overrightarrow{AM} - \overrightarrow{AB} = \frac{1}{2}\overrightarrow{d} - \overrightarrow{b}$
Suy ra $\overrightarrow{AC} . \overrightarrow{BM} = (\overrightarrow{b} + \overrightarrow{d}) . (\frac{1}{2}\overrightarrow{d} - \overrightarrow{b}) = -\overrightarrow{b}^{2} + \frac{1}{2}\overrightarrow{d}^{2} = -1 + \frac{1}{2}.2 = 0$
Từ đó AC $\perp$ BM
b) Theo định lí Pytago ta có $AC^{2} = AB^{2} + BC^{2} = 1^{2} + (\sqrt{2})^{2} = 3$
Suy ra AC = $\sqrt{3}$ và AH = $\frac{1}{\sqrt{3}}$
Suy ra $\overrightarrow{AH} = \frac{1}{3}\overrightarrow{AC}$
N là trung điểm AH nên $\overrightarrow{NB} = \overrightarrow{NA} + \overrightarrow{AB} = \frac{1}{2}\overrightarrow{HA} + \overrightarrow{AB} = \frac{1}{2}[\frac{1}{3}(\overrightarrow{b}+\overrightarrow{d}] + \overrightarrow{b} = \frac{5}{6}\overrightarrow{b} - \frac{1}{6}\overrightarrow{d}$ (1)
P là trung điểm của CD và N là trung điểm HA nên ta có:
$\overrightarrow{ND} = \frac{1}{2}(\overrightarrow{AD} + \overrightarrow{HC}) = \frac{1}{2}[\overrightarrow{d} + \frac{2}{3}(\overrightarrow{b}+\overrightarrow{d}] = \frac{1}{3}\overrightarrow{b} + \frac{5}{6}\overrightarrow{d}$ (2)
Từ (1) và (2) suy ra $\overrightarrow{NB} . \overrightarrow{ND} = (\frac{5}{6}\overrightarrow{b} - \frac{1}{6}\overrightarrow{d}) . (\frac{1}{3}\overrightarrow{b} + \frac{5}{6}\overrightarrow{d}) = 0$
Suy ra NB $\perp$ NP nên tam giác NBP vuông tại N

Bình luận