Giải bài tập 34 trang 78 SBT toán 7 tập 2 cánh diều
Bài 34. Cho điểm M nằm giữa hai điểm O và A. Vẽ các điểm N và B sao cho O là trung điểm của cả AB và MN. Vẽ tia Ox vuông góc với AB, trên tia Ox lấy điểm K. Chứng minh:
a) $\Delta KOM=\Delta KON$;
b) $\Delta KMA=\Delta KNB$.
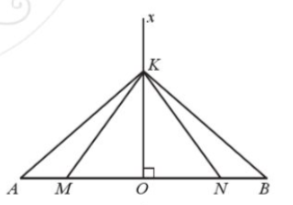
a) Xét tam giác vuông KOM và KON ta có:
KO chung
OM = ON (gt)
$\Delta KOM=\Delta KON$ (hai cạnh góc vuông)
b) Do $\Delta KOM=\Delta KON$ suy ra $\widehat{KMO}=\widehat{KNO}$, KM = KN (1)
Do đó $180-\widehat{KMO}=180-\widehat{KNO}$ hay $\widehat{KMA}=\widehat{KNB}$ (2)
Có OA = OB và OM = On nên OA - OM = OB - ON hay AM = BN (3)
Từ (1) (2) (3) suy ra $\Delta KMA=\Delta KNB $ (c.g.c)

Bình luận