Giải bài tập 33 trang 78 SBT toán 7 tập 2 cánh diều
Bài 33. Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh:
a) $\Delta ABC=\Delta ADE$;
b) DE = BC và DE // BC.
c) $\Delta AEN = \Delta ACM$.
d) M, A, N thẳng hàng.
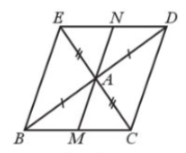
a) Xét tam giác ABC và tam giác ADE ta có:
AB = AD (gt)
$\widehat{BAC}=\widehat{DAE}$
AC = AE (gt)
Suy ra $\Delta ABC=\Delta ADE$ (c.g.c)
b) Do $\Delta ABC=\Delta ADE$ nên BC = DE (hai cạnh tương ứng) và $\widehat{ACB}=\widehat{AED}$ (hai góc tương ứng)
Mặt khác $\widehat{ACB}$ và $\widehat{AED}$ ở vị trí so le trong nên DE // BC.
c) Ta có $EN = \frac{DE}{2};MC=\frac{BC}{2}; DE=BC$ nên EN = MC.
Xét hai tam giác AEN và ACM ta có:
AE = AC
EN = MC
$\widehat{NEA}=\widehat{MCA}$ (so le trong)
Suy ra $\Delta AEN = \Delta ACM$ (c.g.c)
d) Do $\Delta AEN = \Delta ACM$ nên $\widehat{NAE}=\widehat{MAC}$
Ta có: $\widehat{NAM}=\widehat{NAE}+\widehat{EAM}=\widehat{MAC}+\widehat{EAM}=\widehat{EAC}=180^{\circ}$
Vậy M, A, N thẳng hàng.

Bình luận