Giải bài tập 3 trang 70 SBT toán 10 tập 2 kết nối

a) Parabol có đỉnh là I(1; 4) nên có phương trình dạng $y = a(x – 1)^{2} + 4.$

Vì điểm A(2; 3) thuộc parabol nên ta có:

$3 = a(2 – 1)^{2} + 4 ⇔ a + 4 = 3 ⇔ a = – 1.$

Vậy tam thức bậc hai cần tìm là $f(x) = –(x – 1)^{2}+ 4$ hay $f(x) = – x^{2} + 2x + 3.$

Suy ra các hệ số là: a = – 1; b = 2; c = 3.

b) Ta có: a = – 1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh parabol là I(1; 4).

Trục đối xứng x = 1.

Giao điểm của parabol với trục Oy là (0; 3). Điểm đối xứng với điểm (0; 3) qua trục đối xứng x = 1 là (2; 3).

Giao điểm của parabol với trục Ox là (– 1; 0) và (3; 0).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

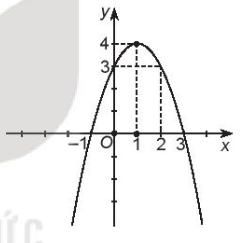
c) Từ đồ thị trên ta thấy:

- Hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).

- Tập giá trị của hàm số là (– ∞; 4].

d) Xét bất phương trình $\frac{f(x)}{x-2}\geq 0$  , hay $\frac{-x^{2}+2x+3}{x-2}\geq 0$ .

Tam thức $f(x) = – x^{2} + 2x + 3$ có $∆' = 12 – (– 1) \times  3 = 4 > 0$ và a = – 1 < 0, f(x) có hai nghiệm phân biệt x1 = – 1 và x2 = 3. Do đó, f(x) > 0 với mọi x ∈ (– 1; 3) và f(x) < 0 với mọi x ∈ (– ∞; – 1) ∪ (3; + ∞).

Ta có bảng xét dấu sau:

 Vậy tập nghiệm của bất phương trình đã cho là S = (– ∞; – 1] ∪ (2; 3].