Giải chi tiết hoạt động thực hành 1 trang 65 chuyên đề toán 12 chân trời sáng tạo

a) Biến ngẫu nhiên 

Các giá trị của X: 0 (không phải mặt 6 chấm) hoặc 1 (mặt 6 chấm). Vậy X là phân bố Bernoulli

- Xác suất xuất hiện mặt 6 chấm: .

- Xác suất không xuất hiện mặt 6 chấm: .

Do đó, X có phân bố Bernoulli với tham số .

Độ lệch chuẩn của X:

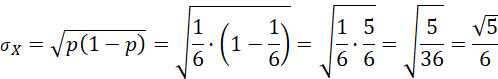
b) 

- Các giá trị của Y : 0 (không có mặt nào 6 chấm) hoặc 1 (có ít nhất một mặt 6 chấm).

- Xác suất xuất hiện ít nhất một mặt 6 chấm: 

  - Xác suất không có mặt nào 6 chấm khi gieo 2 con xúc xắc: .

  - Xác suất có ít nhất một mặt 6 chấm: .

Do đó, Y  có phân bố Bernoulli với tham số

Độ lệch chuẩn:

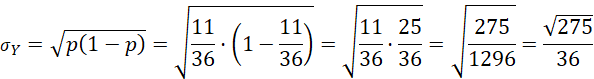
c) 

- Các giá trị của Z : 0 (nếu số chấm chia hết cho 2: 2, 4, 6) hoặc 1 (nếu số chấm không chia hết cho 2: 1, 3, 5).

- Xác suất Z = 0 :

- Xác suất Z = 1 :

Do đó, Z  có phân bố Bernoulli với tham số .

Độ lệch chuẩn:

d) Biến ngẫu nhiên T 

- Các giá trị của T : 0 (nếu số chấm là 3 hoặc 6), 1 (nếu số chấm là 1 hoặc 4), hoặc 2 (nếu số chấm là 2 hoặc 5).

Biến ngẫu nhiên T không có phân bố Bernoulli vì nó có nhiều hơn hai giá trị có thể.