Giải chi tiết bài 6 trang 81 toán 12 tập 2 ctst

A  là biến cố "cả 3 người được chọn đều là kĩ sư"

B  là biến cố "trong 3 người được chọn có ít nhất 2 kĩ sư". 

Chúng ta cần tính xác suất  P(A|B):

Vì  A  (cả 3 người được chọn đều là kĩ sư) là một trường hợp đặc biệt của  B  (có ít nhất 2 kĩ sư trong 3 người được chọn), nên . Do đó, ta có:

P(A)  là xác suất để cả 3 người được chọn đều là kĩ sư.

Số cách chọn 3 kĩ sư từ 4 kĩ sư là 

Tổng số cách chọn 3 người từ 10 người (4 kĩ sư + 6 kĩ thuật viên) là  .

P(B) là xác suất để trong 3 người được chọn có ít nhất 2 kĩ sư.

- Số cách chọn 2 kĩ sư từ 4 kĩ sư và 1 kĩ thuật viên từ 6 kĩ thuật viên là 

- Số cách chọn 3 kĩ sư từ 4 kĩ sư đã tính là 4.

Vậy, tổng số cách thỏa mãn biến cố B  là  36 + 4 = 40 .

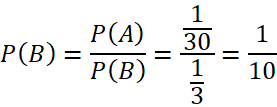
Vậy xác suất để cả 3 người được chọn đều là kĩ sư, biết rằng trong 3 người được chọn có ít nhất 2 kĩ sư, là  .