Câu hỏi tự luận mức độ vận dụng Toán 9 CTST bài 2: Tiếp tuyến của đường tròn

01 Đề bài:

3. VẬN DỤNG (8 câu)

Câu 1: Cho vuông tại A, AH là đường cao, . Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD cắt AC ở E.

a) Chứng minh rằng HE là tiếp tuyến của đường tròn.

b) Tính độ dài đoạn thẳng HE.

Câu 2:Cho tam giác ABC cân tại A nội tiếp đường tròn tâm (O). Vẽ hình bình hành ABCD, tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh rằng :

a) Đường thẳng AD là tiếp tuyến của đường tròn (O).

b) đồng quy.

Câu 3: Cho đường tròn đường kính AB, vẽ  tại trung điểm I của OA. Các tiếp tuyến với đường tròn tại C và D cắt nhau ở M.

a) Chứng minh rằng thẳng hàng.

b) Tứ giác OCAD là hình gì ?

c) Tính .

d) Chứng minh đường thẳng MC là tiếp tuyến của đường tròn .

Câu 4: Cho đường tròn , bán kính OA, dây CD là trung trực của OA. Kẻ tiếp tuyến với đường tròn (O) tại C, tiếp tuyến này cắt đường thẳng OA tại I. 

a) Chứng minh là tam giác đều.                                                         

b) Chứng minh tứ giác OCAD là hình thoi.

c) Tính CI  theo R.             

Câu 5: Cho nửa đường tròn tâm đường kính AB. Một đường thẳng xy tiếp xúc với đường tròn tại C. Gọi D và E lần lượt là hình chiếu của A và B trên xy. Chứng minh rằng:

a) C là trung điểm của DE.

b) Tổng không đổi khi C di động trên nửa đường tròn.

c) Tích .

Câu 6: Cho đường tròn và dây . Vẽ một tiếp tuyến song song với AB, nó cắt các tia OA và OB theo thứ tự tại M và N. Tính diện tích .

Câu 7: Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình vẽ). Cho biết khoảng cách OM là 35 cm.

a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).

b) Tính số đo tạo bởi hai tiếp tuyến AM, BM và số đo (kết quả làm tròn đến phút).

Câu 8: Từ điểm P nằm ngoài đường tròn vẽ hai tiếp tuyến với A và B là các tiếp điểm. Gọi H là chân đường vuông góc vẽ từ A đến đường kính BC. Chứng minh rằng PC cắt AH tại trung điểm I của AH. 

02 Bài giải:

Câu 1: 

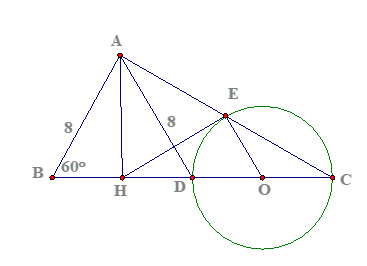
a. Xét

Xét có AH là đường cao đồng thời là đường trung tuyến nên cân tại A, là tam giác đều.

+) Ta có cân tại O

Có: đều

là tiếp tuyến của đường tròn đường kính CD.

b. Xét

Câu 2:

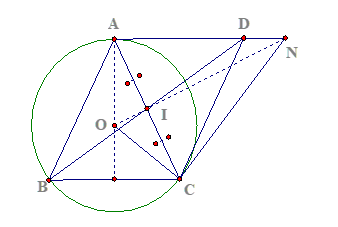
a) Ta có cân tại

Vì tứ giác ABCD là hình bình hành

 

Từ đpcm

b. ) Gọi I là giao điểm của AC và là trung điểm của ( là tiếp tuyến) đồng quy (đpcm).

Câu 3: 

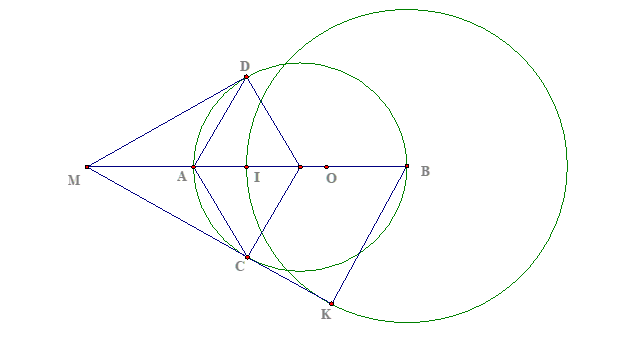
a) AB là trung trực của CD, có (tính chất tiếp tuyến) => m thuộc đường trung trực của thẳng hàng

b) Tứ giác OCAD có hai đường chéo vuông góc tại trung điểm mỗi đường nên là hình thoi

c) có nên là tam giác đều

d) Hạ BK vuông góc MC, ta có: là phân giác

là phân giác của đpcm

(dựa vào tính chất hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

Ta có: là hai góc kề bù, CA là phân giác

là phân giác

d. là hình thoi đều

Câu 4: 

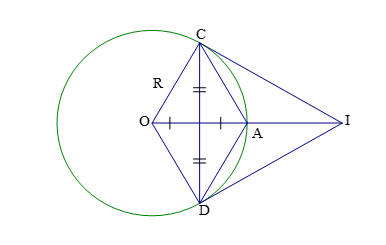
a) Gọi J là giao điểm của OA và CD

Do CD là đường trung trực của OA nên

Vậy là tam giác đều

b) Chứng minh tương tự:

Từ

là hình thoi

c) Xét , ta có:

Câu 5: 

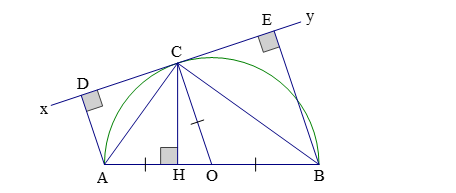
a) Nối OC ta được

Ta có:

Mặt khác

b) Kẻ

Xét hai tam giác vuông và có:

+)

+)

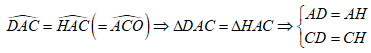
Chứng minh được:

Điểm C nằm trên nửa đường tròn đường kính AB nên vuông tại C

Vậy

Từ 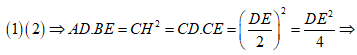đpcm.

Câu 6: 

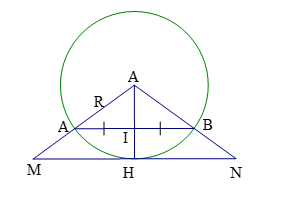
Nối OH ta được (tính chất tiếp tuyến)

Ta lại có

Theo tính chất đường kính vuông góc với một dây ta  được:

Tam giác IOA vuông tại

Xét có (tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng)

Diện tích tam giác MON là:

Câu 7: 

a) Ta có MA, MB lần lượt là hai tiếp tuyến của đường tròn (O; 15 cm) tại A, B và cắt nhau tại M nên MA ⊥ OA, MB ⊥ OB và MA = MB.

Xét ∆OAM vuông tại A, theo định lí Pythagore ta có: OM² = OA² + MA².

Suy ra MA² = OM² – OA² = 35² – 15² = 1000.

Do đó

Vậy .

b) Xét ∆OAM vuông tại A, ta có: .

Suy ra

Vì MA, MB là hai tiếp tuyến của đường tròn (O; 15 cm) cắt nhau tại M nên MA là tia phân giác của góc AMB.

Do đó

Xét tứ giác OAMB có: (tổng các góc của một tứ giác).

Suy ra

Câu 8: 

CA cắt BP tại D; (A thuộc đường tròn đường kính BC)

(tính chất tiếp tuyến)

có , do đó

có có

Từ đpcm.