Câu hỏi tự luận mức độ vận dụng cao Toán 12 cd Bài 2: Phương trình đường thẳng
4. VẬN DỤNG CAO (4 câu)
Câu 1: Cho hai đường thẳng ![]() và
và ![]() và điểm
và điểm ![]() . Gọi
. Gọi ![]() là đường thẳng vuông góc chung của
là đường thẳng vuông góc chung của ![]() và
và ![]() . Gọi
. Gọi ![]() là một điểm thuộc đường thẳng
là một điểm thuộc đường thẳng ![]() thì khi độ dài
thì khi độ dài ![]() ngắn nhất, toạ độ của M bằng bao nhiêu?
ngắn nhất, toạ độ của M bằng bao nhiêu?
Câu 2: Trong không gian với hệ toạ độ ![]() (đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí
(đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí ![]() và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí ![]() trên đường băng
trên đường băng ![]() .
.
a) Lập phương trình đường thẳng ![]() .
.
b) Hãy cho biết góc trượt (góc giữa đường bay ![]() và mặt phẳng nằm ngang
và mặt phẳng nằm ngang ![]() ) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.
) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng ![]() đi qua ba điểm
đi qua ba điểm ![]() ,
, ![]() . Tìm toạ độ của điểm
. Tìm toạ độ của điểm ![]() là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
d) Tìm toạ độ của điểm ![]() trên đoạn thẳng
trên đoạn thẳng ![]() là vị trí mà máy bay ở độ cao 120m.
là vị trí mà máy bay ở độ cao 120m.
e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu ![]() của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

Câu 3: Có một chiếc lồng bằng sắt dạng hình hộp chữ nhật ![]() có
có ![]() . Người thợ hàn muốn hàn một thanh sắt
. Người thợ hàn muốn hàn một thanh sắt ![]() nối hai đoạn
nối hai đoạn ![]() và
và ![]() . Tính chiều dài ngắn nhất của đoạn thanh sắt
. Tính chiều dài ngắn nhất của đoạn thanh sắt ![]() . Làm tròn kết quả đến hàng phần trăm của mét.
. Làm tròn kết quả đến hàng phần trăm của mét.

Câu 4: Cho hình lăng trụ ![]() có
có ![]() là tứ diện đều cạnh
là tứ diện đều cạnh ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Tính tang của góc giữa hai mặt phẳng
. Tính tang của góc giữa hai mặt phẳng ![]() và
và ![]() . Làm tròn kết quả đến hàng phần trăm.
. Làm tròn kết quả đến hàng phần trăm.
Câu 1:
Hai đường thẳng ![]() và
và ![]() có vectơ chỉ phương lần lượt là
có vectơ chỉ phương lần lượt là ![]() và
và ![]()
Gọi ![]() và
và ![]() lần lượt là giao điểm của đường thẳng
lần lượt là giao điểm của đường thẳng ![]() với hai đường thẳng
với hai đường thẳng ![]()
Khi đó ![]() ,
, ![]() ,
, ![]()
Do ![]() là đường thẳng vuông góc chung của
là đường thẳng vuông góc chung của ![]() và
và ![]() nên:
nên:
![]()
![]()
Suy ra ![]()
Vậy phương trình đường thẳng ![]() là:
là: ![]()
Do ![]() là một điểm thuộc đường thẳng
là một điểm thuộc đường thẳng ![]() nên toạ độ của
nên toạ độ của![]() có dạng
có dạng ![]()
![]()
Khi đó ![]()
![]()
Do đó độ dài ![]() ngắn nhất bằng
ngắn nhất bằng ![]()
![]()
Vậy ![]() .
.
Câu 2:
a) Ta có: ![]()
Phương trình đường thẳng ![]() là:
là:
![]()
b) Phương trình mặt phẳng ![]() là
là ![]() . Ta có:
. Ta có:
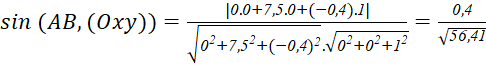
![]()
Vì 2,5° <3° <3,5° nên góc trượt của máy bay nằm trong phạm vi cho phép.
c) Phương trình mặt phẳng ![]() là:
là:
![]()
Vì ![]() thuộc đường thẳng
thuộc đường thẳng ![]() nên
nên ![]() (
(![]() ).
).
Mà ![]() thuộc mặt phẳng
thuộc mặt phẳng ![]() nên
nên
![]()
Suy ra ![]()
d) Vì ![]() thuộc
thuộc ![]() nên
nên ![]() (
(![]() ). Mà
). Mà ![]() có cao độ là
có cao độ là ![]() nên
nên ![]() .
.
Vậy ![]() .
.
e) Ta có: ![]() (km).
(km).
Vì 900 m = 0,9 km < 1,26 km nên phi công không nhìn thấy điểm ![]() và không đạt được quy định an toàn bay.
và không đạt được quy định an toàn bay.
Câu 3:
Chọn hệ trục toạ độ ![]() có gốc toạ độ
có gốc toạ độ ![]() trùng với
trùng với ![]() và
và ![]() ,
, ![]() ,
, ![]() .
.
Phương trình đường thẳng ![]() :
: ![]()
Phương trình đường thẳng ![]() :
: ![]()
![]()
![]()
![]() ngắn nhất khi và chỉ khi
ngắn nhất khi và chỉ khi ![]() và
và ![]()
![]() và
và ![]()
![]() và
và ![]()
![]()
Vậy ![]() (m).
(m).
Câu 4:
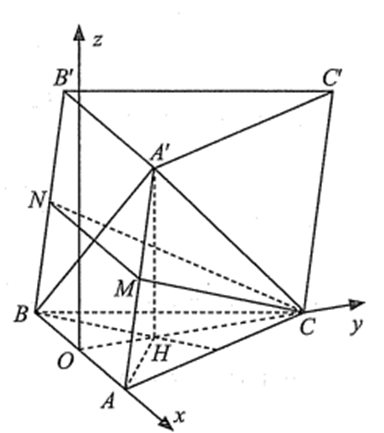
Gọi ![]() là trung điểm của
là trung điểm của ![]() .
.
Chọn hệ trục toạ độ sao cho ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Ta có: ![]() là tứ diện đều cạnh
là tứ diện đều cạnh ![]() nên
nên ![]()
Lại có ![]()
Dễ thấy mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là ![]()
![]() là trung điểm của
là trung điểm của ![]()
![]()
![]() là trung điểm của
là trung điểm của ![]()
![]()
Suy ra ![]() ,
, ![]()
Ta có: ![]()
Do đó mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là ![]()
Khi đó:
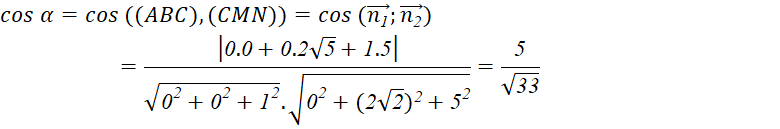
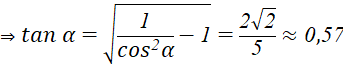
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận