CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ

BÀI 6. CỘNG, TRỪ PHÂN THỨC

1. CỘNG, TRỪ HAI PHÂN THỨC CÙNG MẪU 

HĐKP1:

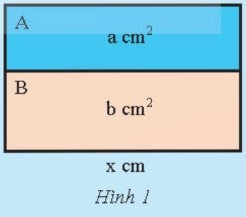
a) Cách 1:

Diện tích của hình chữ nhật lớn là: 

a + b $(cm^{2})$

Chiều rộng của hình chữ nhật lớn là: 

$\frac{a+b}{x}$ (cm).

Cách 2:

Chiều rộng của hình chữ nhật A là: $\frac{a}{x}$ (cm).

Chiều rộng của hình chữ nhật B là: $\frac{b}{x}$ (cm).

Chiều rộng của hình chữ nhật lớn là:

$\frac{a}{x}+\frac{b}{x}$ (cm)

b) Chiều rộng của hình chữ nhật B lớn hơn chiều rộng của hình chữ nhật A là:

$\frac{b}{x}-\frac{a}{x}$ (cm).

=> Kết luận:

Muốn cộng (hoặc trừ) hai phân thức có cùng mẫu, ta cộng (hoặc trừ) các tử thức với nhau và giữ nguyên mẫu thức.

$\frac{A}{C}+\frac{C}{B}=\frac{A+C}{B}$

$\frac{A}{B}-\frac{C}{B}=\frac{A-C}{B}$

Chú ý:

Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.

Ví dụ 1: (SGK – tr31)

Thực hành 1:

a) $\frac{x}{x+3}+\frac{2-x}{x+3}=\frac{x+2-x}{x+3}=\frac{2}{x+3}$

b) $\frac{x^{2}y}{x-y}-\frac{xy^{2}}{x-y}$

$=\frac{x^{2}y-xy^{2}}{x-y}=\frac{xy.(x-y)}{x-y}=xy$

c) $\frac{2x}{2x-y}+\frac{y}{y-2x}$

$=\frac{2x}{2x-y}-\frac{y}{2x-y}=\frac{2x-y}{2x-y}=1$

2. CỘNG, TRỪ HAI PHÂN THỨC KHÁC MẪU 

HĐKP2.

a) $\frac{a+b}{ab}=\frac{a.(a+b)}{ab.a}=\frac{a^{2}+ab}{a^{2}b}$ 

$\frac{a-b}{a^{2}}=\frac{(a-b).b}{a^{2}b}=\frac{a.b-b^{2}}{a^{2}b}$ 

b) A + B 

$= \frac{a^{2}+ab}{a^{2}b}+\frac{ab-b^{2}}{a^{2}b}$

$=\frac{a^{2}+ab+ab-b^{2}}{a^{2}b}$ 

$=\frac{a^{2}+2ab-b^{2}}{a^{2}b}$

A – B 

$=\frac{a^{2}+ab}{a^{2}b}-\frac{ab-b^{2}}{a^{2}b}$

$=\frac{a^{2}+ab-ab+b^{2}}{a^{2}b}$ 

$=\frac{a^{2}+b^{2}}{a^{2}b}$

Nhận xét:

Quy đồng mẫu thức hai phân thức là biến đổi hai phân thức đã cho thành hai phân thức mới có cùng mẫu thức và lần lượt bằng hai phân thức đã cho.

Mẫu thức của các phân thức mới đó gọi là mẫu thức chung của hai phân thức đã cho.

Chú ý: 

Cho hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$.

+ Ta có: $\frac{A}{B}=\frac{A.D}{B.D}$ và $\frac{C}{D}=\frac{B.C}{B.D}$

+ Nếu D là một nhân tử của B (B = D.P với P  là một đa thức) thì lấy mẫu thức chung là B. 

Khi đó, ta quy đồng mẫu thức:

$\frac{C}{D}=\frac{C.P}{D.P} =\frac{C.P}{B}$

(giữ nguyên phân thức $\frac{A}{B}$)

(Tương tự cho trường hợp B  là một nhân tử của D)

+  Nếu B và D có nhân tử chung là E 

 (B = E . M, D = E . N với M và N là những đa thức) thì lấy mẫu thức chung là E . M . N. Khi đó, ta quy đồng mẫu thức:

$\frac{A}{B}=\frac{A.N}{B.N}=\frac{A.N}{E.M.N}$ 

và $\frac{C}{D}=\frac{C.M}{D.M}=\frac{C.M}{E.N.M}$

Ví dụ 2: SGK – tr33

=> Kết luận:

Muốn cộng, trừ hai phân thức khác mẫu thức, ta thực hiện các bước:

- Quy đồng mẫu thức

- Cộng, trừ các phân thức có cùng mẫu thức vừa tìm được.

Ví dụ 3: SGK – tr33

Chú ý:

a) Phép cộng các phân thức cũng có các tính chất giao hoán, kết hợp:

+ $\frac{A}{B}+\frac{C}{D}=\frac{C}{D}+\frac{A}{B}$;

+ $(\frac{A}{B}+\frac{C}{D})+\frac{E}{F}=\frac{A}{B}+(\frac{C}{D}+\frac{E}{F})$;

Nhờ tính chất kết hợp, trong một dãy phép cộng nhiều phân thức, ta không cần đặt dấu ngoặc.

b) Hai phân thức đối nhau khi tổng của chúng bằng 0. Phân thức đối của AB kí hiệu là -$\frac{A}{B}$. Tương tự như với phân số, ta có tính chất:

$-\frac{A}{B}=\frac{-A}{B}=\frac{A}{-B}$

c) Phép trừ phân thức có thể chuyển đổi thành phép cộng phân thức đối:

$\frac{A}{B}-\frac{C}{D}=\frac{A}{B}+(-\frac{C}{D})$

Ví dụ 4. (SGK-tr34)

Thực hành 2. 

a) $\frac{a}{a-3}-\frac{3}{a+3}$

$=\frac{a.(a+3)}{(a-3).(a+3)}-\frac{3.(a-3)}{(a+3).(a-3)}$ 

$=\frac{a.(a+3)}{(a-3).(a+3)}-\frac{3.(a-3)}{(a+3).(a-3)}$ 

$=\frac{a^{2}+3a-3a+9}{a^{2}-9}$ 

$=\frac{a^{2}+9}{a^{2}-9}$ 

b) $\frac{1}{2x}+\frac{2}{x^{2}}=\frac{x}{2x^{2}}+\frac{2.2}{2x^{2}}=\frac{x+4}{2x^{2}}$

c) $\frac{4}{x^{2}-1}-\frac{2}{x^{2}+x}$

$=\frac{4}{(x-1).(x+1)}-\frac{2}{x.(x+1)}$

$=\frac{4x}{x.(x-1).(x+1)}-\frac{2(x-1)}{x.(x-1)(x+1)}$ 

$=\frac{4x-2x+2}{x.(x-1).(x+1)}=\frac{2x+2}{x.(x-1).(x+1)}$

$=\frac{2.(x+1)}{x.(x-1).(x+1)}=\frac{2}{x^{2}-x}$

Thực hành 3. 

$\frac{x}{x+y}+\frac{2xy}{x^{2}-y^{2}}-\frac{y}{x+y}$

$=\frac{x}{x+y}-\frac{y}{x+y}+\frac{2xy}{(x+y).(x-y)}$

$=\frac{x}{x+y}-\frac{y}{x+y}+\frac{2xy}{(x+y).(x-y)}$ 

$=\frac{(x-y)(x+y)+2xy}{(x+y).(x-y)}$ 

$=\frac{(x-y).(x-y)}{(x+y).(x-y)}+\frac{2xy}{(x+y).(x-y)}$ 

$=\frac{(x-y)^{2}+2xy}{(x+y).(x-y)}$ 

$=\frac{x^{2}-2xy+y^{2}+2xy}{x^{2}-y^{2}}$ 

$= \frac{x^{2}+y^{2}}{x^{2}-y^{2}}$

Vận dụng.

Tổng thời gian đi và về là: 

$T = \frac{3}{x+1}+\frac{3}{x-1}=\frac{3.(x-1)+3(x+1)}{x^{2}-1}$

$=\frac{6x}{x^{2}-1}$ (giờ)

Chênh lệch giữa thời gian đi và về là:

$C = \frac{3}{x-1}+\frac{3}{x+1}=\frac{3.(x+1)-3(x-1)}{x^{2}-1}$

$=\frac{6}{x^{2}-1}$ (giờ) 

Khi x = 6km/h, ta  có:

+  $T =\frac{6.6}{6^{2}-1}= \frac{36}{35}$ giờ ($\approx$ 1 giờ 1 phút 43 giây); 

+ $C =\frac{6}{6^{2}-1}= \frac{6}{35}$ giờ ($\approx$ 10 phút 17 giây).