1.GÓC ĐỐI DIỆN VỚI CẠNH LỚN HƠN TRONG MỘT TAM GIÁC

• So sánh hai góc theo cạnh đối diện

HĐ1:

- Độ dài các cạnh theo thứ tự từ bé đến lớn là:

AB < AC < BC.

- Độ dài các góc theo thứ tự từ bé đến lớn là: 

$\widehat{C}<\widehat{B}<\widehat{A}$

- Góc lớn nhất $\widehat{A}$ đối diện với cạnh BC.

- Góc bé nhất $\widehat{C}$ đối diện với cạnh AB.

HĐ2:

$\widehat{B}>\widehat{C}$

Định lí 1:

Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

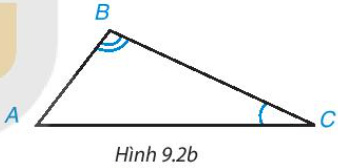
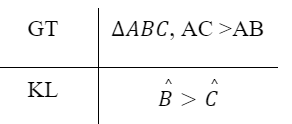
Ví dụ 1: SGK-tr60

Luyện tập 1

Góc đối diện cạnh MN là $\widehat{P}$

Góc đối diện cạnh NP là $\widehat{M}$

Góc đối diện cạnh MP là $\widehat{N}$

Sắp xếp các cạnh từ bé đến lớn ta có MN< NP < MP . Từ đó theo định lí 1 ta có $\widehat{P}<\widehat{M}<\widehat{N}$

2. CẠNH ĐỐI DIỆN VỚI GÓC LỚN HƠN TRONG MỘT TAM GIÁC

• So sánh hai cạnh theo góc đối diện

HĐ3:

Theo hình vẽ, ta có $\widehat{B}$ = 80°; $\widehat{C}$ = 45°. Từ đó ta có $\widehat{B}>\widehat{C}$. Suy ra AC > AB.

HĐ4:

Đúng như dự đoán ở HĐ3, AC >AB.

Định lí 2:

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

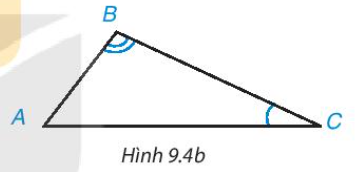
Ví dụ 2 (SGK – tr44)

Luyện tập 2:

Tam giác MNP có $\widehat{M}$ = 47°,  $\widehat{N}$ = 53°

Vậy số đo góc $\widehat{P}$ là : 180°- (53°  + 47°) = 180°  -100° = 80°

Từ đó trong tam giác MNP có $\widehat{M}<\widehat{N}<\widehat{P}$. Theo định lí 2, ta được NP < PM < MN.

Tranh luận:

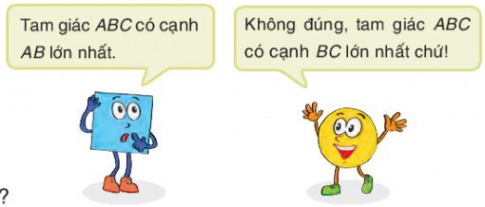
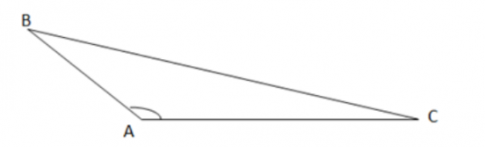
Bạn Tròn nói đúng. Vì góc tù là góc lớn hơn góc vuông và nhỏ hơn tổng 3 góc trong tam giác. Từ đó ta có  90° < $\widehat{A}$ <  180°. Suy ra A là góc lớn nhất trong tam giác ABC

Theo định lí 2, ta được BC là cạnh có độ dài lớn nhất tam giác ABC.

Nhận xét:

- Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với góc vuông (tức cạnh huyền) là cạnh lớn nhất.

- Tương tự trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Vận dụng:

Coi vị trí các cầu thủ mang áo số 4, 2, 3, lần lượt là A, B, C và vị trí quả bóng là D thì: A, B, C thẳng hàng, B ở giữa A và C với $\widehat{ACD}$ là góc tù. Trong tam giác BCD (H 9.2), vì $\widehat{BCD}$ là góc tù nên BD > CD. Cũng vì $\widehat{BCD}$ là góc tù nên $\widehat{CBD}=\widehat{B_{1}}$ phải là góc nhọn (do tổng số đo ba góc trong tam giác bằng 180°), từ đó góc kề bù với nó là $\widehat{ABD}=\widehat{B_{2}}$ phải là góc tù. Trong tam giác ABD, vì góc $\widehat{B_{2}}$ tù nên AD > BD. Vậy AD > BD > CD. Từ đó, cầu thủ mang áo số 3 gần quả bóng nhất, cầu thủ mang áo số 4 xa quả bóng nhất.