I. ĐỊNH NGHĨA 

HĐ1: Ta có:

$\frac{12}{28}=\frac{12:4}{28:4}=\frac{3}{7}$; 

$\frac{7,5}{17,5}=\frac{75}{175}=\frac{75:25}{175:25}=\frac{3}{7}$

Vậy $\frac{12}{28}=\frac{7,5}{17,5}$

Kết luận: Tỉ lệ thức là đẳng thức của hai tỉ số $\frac{a}{b}$ và $\frac{c}{d}$ viết là $\frac{a}{b}=\frac{c}{d}$

Ví dụ 1: (SGK – tr52)

Luyện tập 1: 

a) Ta có: 

$\frac{-2}{5}: 4 = \frac{-2}{5}.\frac{1}{4}=\frac{-2}{10}=\frac{-1}{10}$

$\frac{3}{4}:\frac{-15}{2}=\frac{3}{4}.\frac{-2}{15}=\frac{-6}{60}=\frac{-1}{10}$

Vì $\frac{-2}{5}: 4 = \frac{-1}{10}$ và Vì $\frac{3}{4}:\frac{-15}{2} = \frac{-1}{10}$

=> Lập được tỉ lệ thức.

b) Ta có: 

$\frac{15}{27}=\frac{15:3}{27:3}=\frac{5}{9}$;

$25:30=\frac{25}{30}=\frac{25:5}{30:5}=\frac{5}{6}$

Vì $\frac{5}{9}\neq \frac{5}{6}$ nên $\frac{15}{27}$ và 25:30 không lập được tỉ lệ thức.

II. TÍNH CHẤT 

1. Tính chất 1 

HĐ2: 

a) Ta có: 6. (-15) = -90;             10.(-9) =  - 90

Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9

b) Nhân hai vế của tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ với tích bd, ta được:

$\frac{a.b.d}{b}=\frac{c.b.d}{d}$ => ad = bc

Vậy ta được đằng thức ad = bc

Kết luận: Nếu $\frac{a}{b}=\frac{c}{d}$ thì ad = bc.

Ví dụ 2: (SGK – tr53)

Luyện tập 2:

Vì (-0,4) : x = 1,2 : 0,3 nên  

$\frac{-0,4}{x}=\frac{1,2}{0,3}$ => (-0,4).0,3 = 1,2.x 

x = $\frac{(-0,4).0,3}{1,2}$ = -0,1 

Vậy x = -0,1  

2. Tính chất 2 

HĐ3

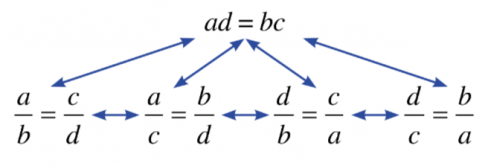
Kết luận: Nếu ad = bc và a, b, c, d đều khác 0 thì ta có các tỉ lệ thức: 

$\frac{a}{b}=\frac{c}{d};\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}$

Nhận xét: Với a, b, c, d đều khác 0 thì từ một trong năm đẳng thức sau đây, ta có thể suy ra các đẳng thức còn lại. 

Ví dụ 3: (SGK – 54)

Luyện tập 3.

a) Ta được: 18.21 = 27.14

b) Từ 4 số: 14; 18; 21; 27, ta có đẳng thức sau: 18.27=21.14, ta lập được các tỉ lệ thức:

$\frac{18}{27}=\frac{14}{21};\frac{18}{14}=\frac{27}{21};\frac{21}{27}=\frac{14}{18};\frac{21}{14}=\frac{27}{18}$