I. QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN TRONG MỘT TAM GIÁC 

1. Góc đối diện với cạnh lớn hơn 

Trong tam giác ABC, góc A được gọi là góc đối diện với cạnh BC 

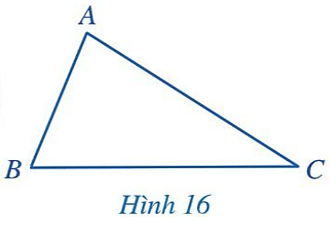
HĐ1: SGK trang 74

a) AB < AC

b) $\widehat{B}>\widehat{C}$

Kết luận: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn. 

Ví dụ 1. SGK – tr74

LT1. 

Góc $\widehat{N}$ là góc lớn nhất (Vì là góc đối diện cạnh MP dài nhất trong tam giác)

Góc $\widehat{P}$ là góc nhỏ nhất (Vì là góc đối diện cạnh MN nhỏ nhất trong tam giác)

2. Cạnh đối diện với góc lớn hơn

Trong tam giác ABC, cạnh BC được gọi là cạnh đối diện với góc A

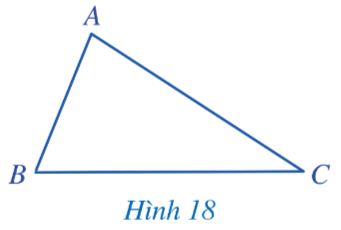
HĐ2: SGK trang 75

a) $\widehat{B}>\widehat{C}$

b) AB < AC (vì $\widehat{B}>\widehat{C}$)

Kết luận: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. 

Ví dụ 2. SGK – tr75

Nhận xét: 

• Trong tam giác vuông, cạnh huyền là cạnh lớn nhất 
• Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất. 

LT2. 

a) DE < DG (do DG là cạnh đối diện với góc tù nên DG lớn nhất)

b) Xét tam giác MNP có: 

$\widehat{M}+\widehat{N}+\widehat{P}$ = 180° (tổng ba góc trong tam giác)

<=> 56° + 65° + $\widehat{P}$  = 180° 

<=> $\widehat{P}$ = 180° - 121° = 59° 

Vì 65° > 59° > 56°

=> $\widehat{N}>\widehat{M}>\widehat{P}$ 

Vậy NP là cạnh nhỏ nhất; MP là cạnh lớn nhất

II. BẤT ĐẲNG THỨC TAM GIÁC 

HĐ3: SGK – tr75

Dự đoán: bạn An đi thẳng từ nhà đến trường sẽ gần hơn.

HĐ4: SGK – tr75

a) HS tự kiểm tra

b) AB + BC > AC (do 5 > 4)

Kết luận: Tromg một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại. 

Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại. 

Ví dụ 3. SGK – tr76 

LT3. 

Xét tam giác ABC 

Có AB + BC > AC (bất đẳng thức tam giác)

=> 6 > AC   (1)

Lại có: BC – AB < AC (hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại)

=> 2 < AC (2)

Từ (1) và (2) => 2 < AC < 6 

Vậy AC > AB