Lý thuyết trọng tâm toán 7 cánh diều bài 1: Hình hộp chữ nhật. Hình lập phương
Tổng hợp kiến thức trọng tâm toán 7 cánh diều bài 1: Hình hộp chữ nhật. Hình lập phương. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
I. HÌNH HỘP CHỮ NHẬT
HĐ1:
a) Vẽ hình 1.
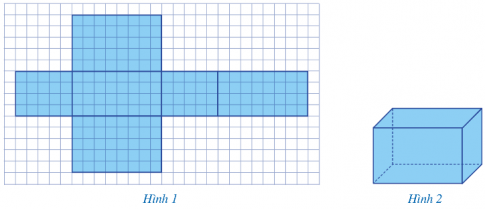
b) Cắt, gấp để tạo lập hình 2.
c) Hình hộp chữ nhật ở Hình 2 có 6 mặt, 12 cạnh và 8 đỉnh.
Nhận xét: Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh.
HĐ2:
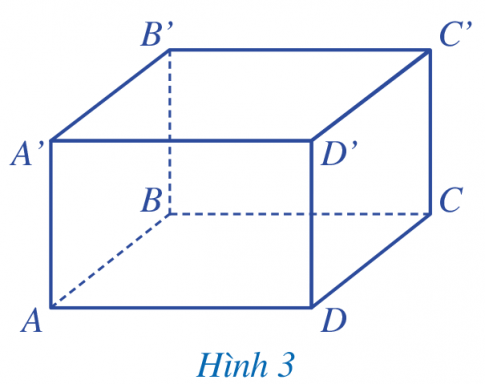
Hình hộp chữ nhật ABCD. A’B’C’D’ có:
- Gồm có 6 mặt: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
- Gồm có 12 cạnh: AB; BC; CD; DA; A’B’; B’C’; C’D’; D’A’; AA’; BB’; CC’; DD’.
- Gồm có 8 đỉnh: A; B; C; D; A’; B’; C’; D’.
Kết luận: Ở Hình 3 ta có:
- Hình hộp chữ nhật ABCD.A'B'C'D';
- Đáy dưới ABCD, đáy trên A'B'C'D';
Các mặt bên: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
Các cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A';
Các cạnh bên: AA', BB', CC', DD';
Các đỉnh: A, B, C, D, A', B', C', D'.
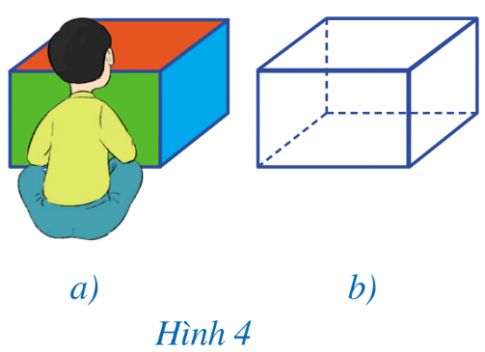
Chú ý: Khi ngồi trước một hình hộp chữ nhât như ở Hình 4a, ta chỉ nhìn thấy ba mặt được tô màu, còn một số cạnh không nhìn thấy được. Tuy nhiên, để nhận dạng tốt hơn cả hình hộp chữ nhật, người ta vẫn vẽ các cạnh không nhìn thấy đó, nhưng bằng nét đứt (như Hình 4b).
HĐ3:
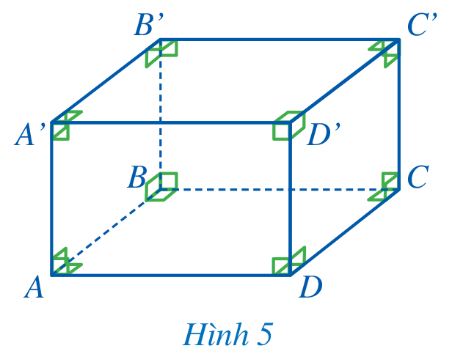
a) Mặt AA’D’D là hình chữ nhật.
b) Hai cạnh bên AA’ và DD’ có độ dài bằng nhau.
Nhận xét: Hình hộp chữ nhật có:
- Các mặt đều là hình chữ nhật;
- Các cạnh đều bằng nhau.
HĐ4: SGK trang 77
Nhận xét: Hình hộp chữ nhật có 4 đường chéo.
II. HÌNH LẬP PHƯƠNG
HĐ5: SGK trang 78
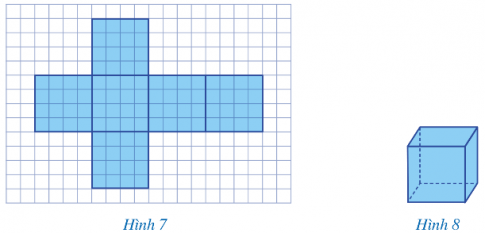
Nhận xét: Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
HĐ6:
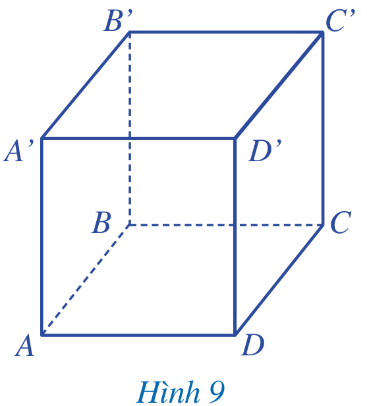
Hình lập phương ABCD. A’B’C’D’ có:
- 6 mặt: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
- 12 cạnh: AB; BC; CD; DA; A’B’; B’C’; C’D’; D’A’; AA’; BB’; CC’ ; DD’.
- 8 đỉnh: A; B; C; D; A’; B’; C’; D’.
- 4 đường chéo: AC’; A’C; BD’; B’D.
HĐ7:
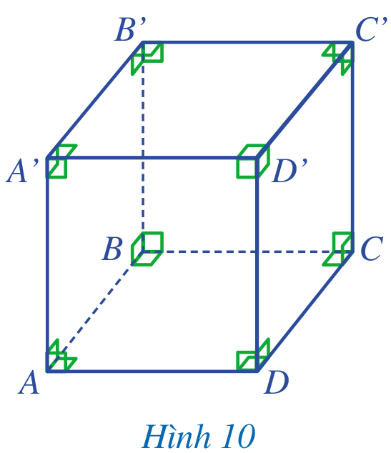
a) Mặt AA’D’D là hình gì vuông.
b) Các cạnh của hình lập phương đó bằng nhau.
Nhận xét: Hình lập phương có:
- Các mặt đều là hình vuông;
- Các cạnh đều bằng nhau.
III. DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH HÌNH HỘP CHỮ NHẬT, HÌNH LẬP PHƯƠNG
Kết luận:
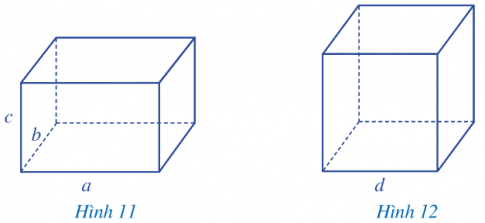
Ta có một số công thức sau:
Diện tích xung quanh | Thể tích | |
Hình hộp chữ nhật | Sxq = 2(a + b)c | V = abc |
Hình lập phương | Sxq = 4d$^{2}$ | V = d$^{3}$ |
Ví dụ 1: SGK trang 79
Luyện tập:
Diện tích xung quanh của viên gạch là:
2. (220 + 105). 65 = 42 250(mm$^{2}$)
Thể tích của viên gạch là:
220. 105. 65 = 1 501 500 (mm$^{3}$)= 15 015 cm$^{3}$
Ví dụ 2: SGK trang 79
Bình luận