CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC

BÀI 3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ

1. GIẢI TAM GIÁC

Định nghĩa:

Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.

Ví dụ 1 (SGK - 74)

Thực hành:

a) Ta có: $\widehat{A}$ = 180° - $\widehat{B}$ - $\widehat{C}$ 

= 180° - 44°30’ - 64° = 71°30’

Áp dụng định lí sin, ta có:

$\frac{a}{sinA}$ = $\frac{b}{sinB}$= $\frac{c}{sinC}$

⟹ b = $\frac{a.sinB}{sinA}$ = $\frac{17,4.sin44°30'}{sin71°30'}$ ≈ 12,9

      c = $\frac{a.sinB}{sinA}$ = $\frac{17,4.sin64°}{sin71°30'}$ ≈ 16,5

b) Áp dụng hệ quả định lí côsin, ta có:

cosA = $\frac{b^{2}+c^{2}-a^{2}}{2bc}$ =$\frac{6^{2}+8^{2}-10^{2}}{2.6.8}$= 0

⟹ $\widehat{A}$ = 90°

Áp dụng định lí sin, ta có: $\frac{a}{sinA}$ = $\frac{b}{sinB}$

⟹ sinB = $\frac{bsinA}{a}$ = $\frac{6.sin90°}{10}$ = $\frac{3}{5}$

⟹ $\widehat{B}$ = 36°52’

⟹ $\widehat{C}$ = 180° - 90° - 36°52’ = 53°8’

2. ÁP DỤNG GIẢI TAM GIÁC VÀO THỰC TẾ 

Ví dụ 2 (SGK - tr75)

Ví dụ 3 (SGK - tr75)

Ví dụ 4 (SGK - tr76)

Ví dụ 5 (SGK - tr76)

Vận dụng 1: 

Đổi 90’ = 1,5h

Quãng đường máy bay thứ nhất bay được sau 90 phút là: OA = 450. 1,5 = 675 (km)

Quãng đường máy bay thứ hai bay được sau 90 phút là: OB = 630. 1,5 = 945 (km)

Ta có: $\widehat{AOB}$ = 90° - 25° = 65°

Áp dụng định lí côsin, ta có:

AB$^{2}$ = OA$^{2}$ + OB$^{2}$ - 2. OA. OB. cos$\widehat{AOB}$

= 675$^{2}$ + 945$^{2}$ - 2. 675. 945. cos65°

≈ 809494,75 ⟹ AB ≈ 889,7 (km)

Vậy sau 90 phút, hai máy bay cách nhau khoảng 899,7 km.

Vận dụng 2:

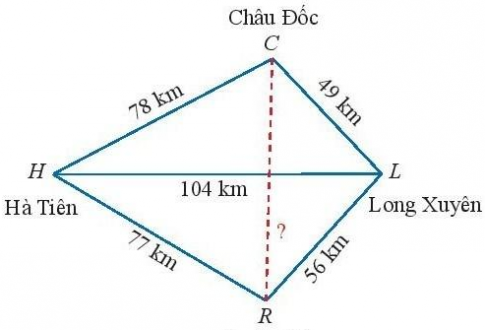
Áp dụng hệ quả định lí côsin, ta có:

cos$\widehat{CHL}$= $\frac{HC^{2}+HL^{2}-CL^{2}}{2.HC.HL}$ =$\frac{78^{2}+104^{2}-49^{2}}{2.78.104}$≈ 0,89

⟹ $\widehat{CHL}$ = 26°39’

cos$\widehat{LHR}$ = $\frac{HL^{2}+HR^{2}-RL^{2}}{2.HL.HR}$ =$\frac{104^{2}+77^{2}-56^{2}}{2.104.77}$≈ 0,85

⟹ $\widehat{LHR}$ = 31°49’

⟹ $\widehat{CHR}$ = $\widehat{CHL}$ + $\widehat{LHR}$ ≈ 26°39’ + 31°49’

= 58°28’

Áp dụng định lí côsin, ta có:

CR$^{2}$ = HC$^{2}$ + HR$^{2}$  - 2HC. HR. cos$\widehat{CHR}$

= 78$^{2}$ + 77$^{2}$ - 78. 77. cos58°28’ ≈ 5730,79

⟹ CR ≈ 75,7 (km)

Vậy Châu Đốc và Rạch Giá cách nhau khoảng 75,7 km.