CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

1. KHÁI NIỆM BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HĐKP 1: 

a. 20x + 50y.

b. 20x + 50y là tổng số tiền bạn Nam đã ủng hộ. Vì Nam để dành được 700 nghìn đồng nên tổng số tiền Nam ủng hộ chỉ có thể nhỏ hơn hoặc bằng 700 nghìn.

Kết luận:

Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng

ax+by+c<0,ax+by+c>0

ax+by+c≤0; ax+by+c≥0.

trong đó a, b, c là những số cho trước; a, b không đồng thời bằng 0 và x, y là các ẩn.

Ví dụ 1 (SGK – tr29)

Thực hành 1:

Các bất phương trình bậc nhất hai ẩn là: a, b, c.

2. NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HĐKP 2:

Trường hợp 1 thỏa mãn tình huống nêu trong Khám phá 1. 

Vì: 2. 20 + 3. 50 = 190 < 700

Kết luận:

Xét bất phương trình ax+by+c<0.

Mỗi cặp số (x$_{0}$;y$_{0}$) thỏa mãn ax$_{0}$+by$_{0}$+c<0 được gọi là nghiệm của bất phương trình đã cho.

Chú ý: Nghiệm của các bất phương trình
ax+by+c>0, ax+by+c≤0

ax+by+c≥0

được định nghĩa tương tự.

Nhận xét: 

Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

Ví dụ 2 (SGK- tr 30)

Thực hành 2:

a. Vì 4. 9 - 7. 1 - 28 = 1 > 0 nên (9; 1) là nghiệm của bất phương trình.

b. Vì 4. 2 - 7. 6 - 28 = -62 < 0 nên (2; 6) không là nghiệm của bất phương trình.

c. Vì 4. 0 - 7. (-4) - 28 = 0 nên (0; - 4) là nghiệm của bất phương trình.

Vận dụng:

a) $\frac{26,1}{100}$x+5,7y≤60;
b) $\frac{26,1.150}{100}$+5,7⋅2=50,55<60 : Phù hợp;

 $\frac{26,1.200}{100}$+5,7⋅2=63,6>60 : Không phù hợp.

3. BIỂU DIỄN MIỀN NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HĐKP 3:

a)

b) 

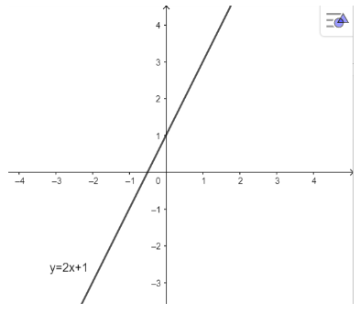
+ Có: 2. (-2) - 0 + 1 = -3 < 0 nên (-2; 0) là nghiệm của bất phương trình 2x - y + 1 < 0.

+ Có: 2. 0 - 0 + 1 = 1 > 0 nên (0; 0) không là nghiệm của bất phương trình 2x - y + 1 < 0.

+ Có: 2. 1 - 1 + 1 = 2 > 0 nên (1; 1) không là nghiệm của bất phương trình 2x - y + 1 < 0.

Kết luận:

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x$_{0}$;y$_{0}$) sao cho mãn ax$_{0}$+by$_{0}$+c<0 được gọi là miền nghiệm của bất phương trình ax+by+c<0.

- Người ta chứng minh được rằng đường thẳng d có phương trình ax + by = c chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng bờ d:

+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ (x; y) thỏa mãn ax+by>c

+ Nửa mặt phẳng còn lại (không kể bờ d) gồm các điểm có tọa độ (x; y) thỏa mãn ax + by <c.

Bờ d gồm các điểm có tọa độ (x; y) thỏa mãn ax + by = c.

Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax+by+c<0:

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng Δ:ax+by+c=0.

Bước 2: Lấy một điểm (x$_{0}$;y$_{0}$) không thuộc . Tính ax$_{0}$+by$_{0}$+c.

Bước 3: Kết luận

- Nếu ax$_{0}$+by$_{0}$+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ) chứa điểm (x$_{0}$;y$_{0}$).

- Nếu ax$_{0}$+by$_{0}$+c<0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ .) không chứa điểm (x$_{0}$;y$_{0}$).

Chú ý:

Đối với các bất phương trình bậc nhất hai ẩn dạng ax+by+c≤0

(hoặc ax+by+c≥0)  thì miền nghiệm là miền nghiệm của bất phương trình ax+by+c<0 (hoặc ax+by+c>0) kể cả bờ.

Ví dụ 3 (SGK - tr31)

Thực hành 3:

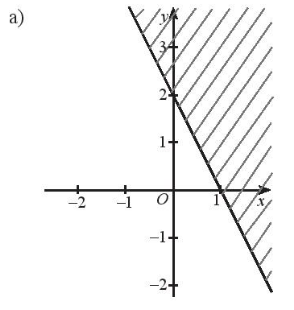
a) Vẽ đường thẳng d: 2x + y - 2 = 0 đi qua hai điểm A(0; 2) và B(1; 0).

Xét gốc tọa độ O(0; 0). Ta thấy O ∉ d và 2.0 +0 - 2 = -2 < 0. Do đó, miền nghiệm của bất phương trình 2x + y - 2 ≤ 0 là nửa mặt phẳng kể cả bờ d, chứa gốc tọa độ O (miền không gạch chéo trong hình).

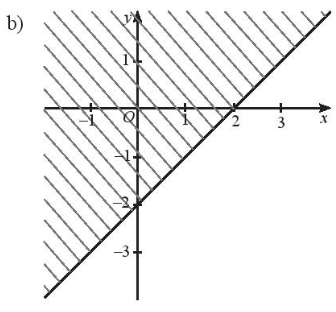
b) Vẽ đường thẳng d': x - y - 2 = 0 đi qua hai điểm A(0; -2) và B(2; 0).

Xét gốc tọa độ O(0;0). Ta thấy O ∉ d' và 0 - 0 - 2 < 0. Do đó, miền nghiệm của bất phương trình x - y - 2 ≥ 0 là nửa mặt phẳng kể cả bờ d', không chứa gốc tọa độ O (miền không tô xanh trong hình).

Vận dụng 2: 

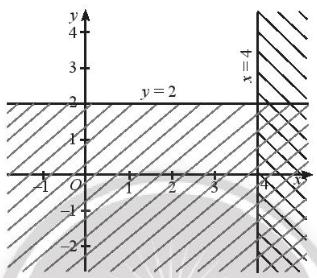
a. Vẽ đường thẳng Δ: y = 2. Miền nghiệm của bất phương trình y ≥ 2 là nửa mặt phẳng kể cả bờ Δ, không chứa gốc tọa độ O. 

b. Vẽ đường thẳng Δ': x = 4. Miền nghiệm của bất phương trình x ≤ 4 là nửa mặt phẳng kể cả bờ Δ', chứa gốc tọa độ O.