1. TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ

Hoạt động 1: Cho vecto $\overrightarrow{AB}= \overrightarrow{a}$. Hãy xác định điểm C sao cho $\overrightarrow{BC}= \overrightarrow{a}$.

a. Tìm mối quan hệ giữa $\overrightarrow{AB}$ và $\overrightarrow{a} +\overrightarrow{a}$

b. Vecto $\overrightarrow{a} +\overrightarrow{a}$ có mối quan hệ như thế nào về hướng và độ dài đối với vecto $\overrightarrow{a}$?

Hướng dẫn giải:

Điểm C nằm trên tia AB sao cho BC = a. 

a. $\overrightarrow{a} +\overrightarrow{a}$= $\overrightarrow{AC}$

Vậy vecto $\overrightarrow{a} +\overrightarrow{a}$ cùng hướng và có độ dài gấp đôi so với vecto $\overrightarrow{AB}$

b. Vậy vecto $\overrightarrow{a} +\overrightarrow{a}$ cùng hướng và có độ dài gấp đôi so với vecto $\overrightarrow{a}$

Câu hỏi: $1\overrightarrow{a}$ và $\overrightarrow{a}$ có bằng nhau hay không?

Hướng dẫn giải:

Có bằng nhau.

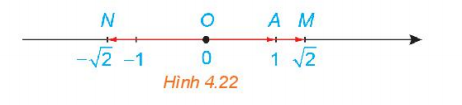
Hoạt động 2: Trên một trục số gọi O, A, M, N tương ứng biểu thị các số 0; 1; $\sqrt{2}; -\sqrt{2}$. Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto $\overrightarrow{OM}, \overrightarrow{ON}$ với vecto $\overrightarrow{a}= \overrightarrow{OA}$. Viết đẳng thức thể hiện mối quan hệ giữa hai vecto $\overrightarrow{OM}, \overrightarrow{OA}$.

Hướng dẫn giải:

• $\overrightarrow{OM}$ và $\overrightarrow{a}$ cùng hướng, độ dài của $|\overrightarrow{OM}|=\sqrt{2}|\overrightarrow{a}|$.
• $\overrightarrow{ON}$ và $\overrightarrow{a}$ ngược hướng, độ dài của $|\overrightarrow{ON}|=\sqrt{2}|\overrightarrow{a}|$.
• $\overrightarrow{OM}=\sqrt{2}\overrightarrow{a}$.

Câu hỏi: $-\overrightarrow{a}$ và $(-1)\overrightarrow{a}$ có mối quan hệ gì?

Hướng dẫn giải:

$-\overrightarrow{a}$ = $(-1)\overrightarrow{a}$

Luyện tập 1: Cho đường thẳng d đi qua hai điêm phân biệt A và B. Những khẳng định nào sau đây là đúng?

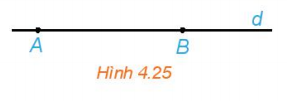
a. Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để $\overrightarrow{AM}=t\overrightarrow{AB}$.

b. Với điểm M bất kì, ta luôn có $\overrightarrow{AM}=\frac{AM}{AB}\overrightarrow{AB}$

c. Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số $t\leq 0$ để $\overrightarrow{AM}=t\overrightarrow{AB}$.

Hướng dẫn giải:

Khẳng định đúng: a, c.

2. CÁCH TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ

Hoạt động 3: Với $\overrightarrow{u}\neq \overrightarrow{0}$ và hai số thực k, t, những khẳng định nào sau đây đúng?

a. Hai vecto k(t$\overrightarrow{u}$) và (kt)$\overrightarrow{u}$ có cùng độ dài bằng |kt||$\overrightarrow{u}$|.

b. Nếu kt$\geq 0$ thì cả hai vecto k(t$\overrightarrow{u}$), (kt)$\overrightarrow{u}$ cùng hướng với $\overrightarrow{u}$.

c. Nếu kt < 0 thì cả hai vecto k(t$\overrightarrow{u}$), (kt)$\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

d. Hai vecto k(t$\overrightarrow{u}$), (kt)$\overrightarrow{u}$ bằng nhau.

Hướng dẫn giải:

Khẳng định đúng: a, b, c, d.

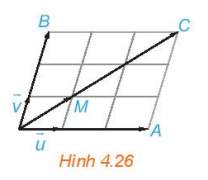
Hoạt động 4: Hãy chỉ ra trên Hình 4.26 hai vecto 3($\overrightarrow{u}+\overrightarrow{v}$) và 3$\overrightarrow{u}$+3$\overrightarrow{u}$. Từ đó, nêu mối quan hệ giữa 3($\overrightarrow{u}+\overrightarrow{v}$ và 3$\overrightarrow{u}$+3$\overrightarrow{u}$

Hướng dẫn giải:

• 3($\overrightarrow{u}+\overrightarrow{v}$) : $\overrightarrow{OC}$ 
• 3$\overrightarrow{u}$+3$\overrightarrow{u}$: $\overrightarrow{OC}$ .
• 3($\overrightarrow{u}+\overrightarrow{v}$) =3$\overrightarrow{u}$+3$\overrightarrow{u}$

Luyện tập 2: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có: $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$

Hướng dẫn giải:

Vì G là trọng tâm tam giác ABC nên ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

=> $\overrightarrow{OA}-\overrightarrow{OG}+\overrightarrow{OB}- \overrightarrow{OG}+\overrightarrow{OC}- \overrightarrow{OG}=\overrightarrow{0}$

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$

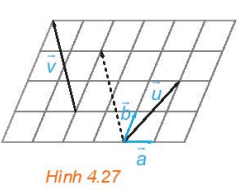
Luyện tập 3: Trong hình 4.27, hãy biểu thị mỗi vecto $\overrightarrow{u},\overrightarrow{v}$ theo hai vecto $\overrightarrow{a},\overrightarrow{b}$, tức là tìm các số x, y, z, t để $\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b}$, $\overrightarrow{v}=t\overrightarrow{a}+z\overrightarrow{b}$.

Hướng dẫn giải:

• $\overrightarrow{u}=2\overrightarrow{a}+2\overrightarrow{b}$,
• $\overrightarrow{v}=-2\overrightarrow{a}+3\overrightarrow{b}$.