1. TỔNG CỦA HAI VECTƠ

Hoạt động 1: Với hai vecto $\overrightarrow{a}, \overrightarrow{b}$ cho trước, lấy một điểm A và vẽ các vecto $\overrightarrow{AB}= \overrightarrow{a}, \overrightarrow{BC}=\overrightarrow{b}$. Lấy điểm A' khác A và cũng vẽ các vecto $\overrightarrow{A'B'} = \overrightarrow{a}, \overrightarrow{B'C'} = \overrightarrow{b}$. Hỏi hai vecto $\overrightarrow{AC}$ và $\overrightarrow{A'C'}$ có mối quan hệ gì?

Hướng dẫn giải:

$\overrightarrow{AC}$= $\overrightarrow{A'C'}$ 

Hoạt động 2: Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vecto $\overrightarrow{AB}+\overrightarrow{AD} $ và $\overrightarrow{AC}$ .

Hướng dẫn giải:

$\overrightarrow{AB}+\overrightarrow{AD} $= $\overrightarrow{DC}+\overrightarrow{AD} $= $\overrightarrow{AC}$.

Vậy $\overrightarrow{AB}+\overrightarrow{AD} $ = $\overrightarrow{AC}$.

Hoạt động 3: 

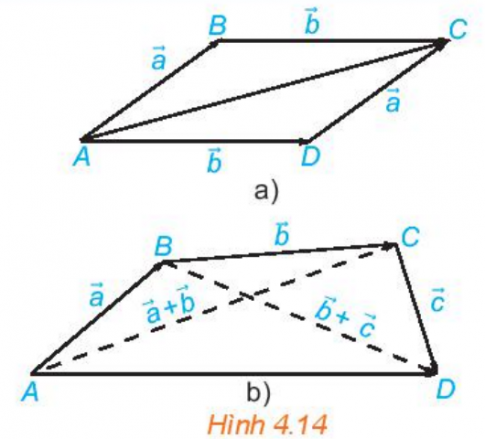
a. Trong Hình 4.14a, hãy chỉ ra vecto $\overrightarrow{a}+\overrightarrow{b} $ và vecto $\overrightarrow{b}+\overrightarrow{a} $ 

b. Trong Hình 4.14b, hãy chỉ ra vecto $(\overrightarrow{a}+\overrightarrow{b}) +\overrightarrow{c} $ và vecto $\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c} )$

Hướng dẫn giải:

a.

• $\overrightarrow{a}+\overrightarrow{b} $ = $\overrightarrow{AC}$
• $\overrightarrow{b}+\overrightarrow{a} $ = $\overrightarrow{AC}$.

b.

• $(\overrightarrow{a}+\overrightarrow{b}) +\overrightarrow{c} $= $\overrightarrow{AD}$
• $\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c} )$ = $\overrightarrow{AD}$

Luyện tập 1: Cho hình thoi ABCD với cạnh có độ dài bằng 1 và $\widehat{BAD}=120^{o}$. Tính độ dài của các vecto $\overrightarrow{CB}+\overrightarrow{CD}$, $\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA} $.

Hướng dẫn giải:

• $\overrightarrow{CB}+\overrightarrow{CD}$ = $\overrightarrow{CA}$
• Dựng hình bình hành ACDE.

$\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA} $= $\overrightarrow{DB}+\overrightarrow{BA}+\overrightarrow{CD} $= $\overrightarrow{DA}+\overrightarrow{CD} $ = $\overrightarrow{DE} $ = $\overrightarrow{CA} $

(do ACDE là hình bình hành).

• Tính độ dài đoạn AC:

Do ABCD là hình thoi có góc $\widehat{BAD}=120^{o}$ nên $\widehat{ADC}=60^{o}$

Suy ra tam giác ACD là tam giác đều, nên AC = CD = 1.

Vậy độ dài của các vecto $\overrightarrow{CB}+\overrightarrow{CD}$, $\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA} $ đều bằng 1.

2. HIỆU CỦA HAI VECTƠ

Hoạt động 4: Thế nào là hai lực cân bằng? Nếu dùng hai vecto để biểu diễn hai lực cân bằng thì hai vecto này có mối quan hệ gì với nhau?

Hướng dẫn giải:

Hai lực cân bằng là hai lực mạnh như nhau, có cùng phương nhưng ngược chiều, tác dụng vào cùng một vật.

Hai vecto sẽ ngược hướng nhau, điểm đầu của vecto này là điểm cuối của vecto kia và có độ dài bằng nhau.

Luyện tập 2: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng $\overrightarrow{OA}+ \overrightarrow{OB}+ \overrightarrow{OC}+ \overrightarrow{OD}= \overrightarrow{O}$.

Hướng dẫn giải:

Do M là trung điểm của AB nên ta có: $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{O}$, 

=> $\overrightarrow{OA}-\overrightarrow{OM}+\overrightarrow{OB}-\overrightarrow{OM}=\overrightarrow{O}$

hay: $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OM}$

Tương tự ta có: $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{ON}$

Suy ra: $\overrightarrow{OA}+ \overrightarrow{OB}+ \overrightarrow{OC}+ \overrightarrow{OD}= \overrightarrow{O}$ = $2\overrightarrow{OM} + 2\overrightarrow{ON}=\overrightarrow{O}$

Vận dụng: Tính lực kéo cần thiết một khẩu pháo có trọng lượng 22148 N (ứng với khối lượng xấp xỉ 2260 kg) lên một con dốc nghiêng 30^o so với phương nằm ngang. Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?

Hướng dẫn giải:

$|\overrightarrow{P}|=22148 = OA$.

Hợp lực của $\overrightarrow{P}$ và $\overrightarrow{w}$ là $\overrightarrow{OC}$.

Xét tam giác vuông OCA vuông tại C, có góc $\widehat{CAC}=30^{o}$, ta có: OC = OA.sin$30^{o}$ = 22148.$\frac{1}{2}$ = 11074.

=> $|\overrightarrow{OC}|$ = 11074.

Để kéo khẩu pháo lên với lực F thì ta có: $|\overrightarrow{F}| > |\overrightarrow{P}+ \overrightarrow{w}|$

Hay: $|\overrightarrow{F}| > 11074$.

Nếu lực kéo của mỗi người bằng 100N thì cần ít nhất 111 người để kéo pháo.