CHƯƠNG IV: VECTƠ

BÀI 8. TỔNG VÀ HIỆU CỦA HAI VECTƠ

1. TỔNG CỦA HAI VECTƠ

HĐ1:   $\underset{AC}{\rightarrow}$=$\underset{A'C'}{\rightarrow}$

Định nghĩa:

Cho hai vectơ $\underset{a}{\rightarrow}$,$\underset{b}{\rightarrow}$. Lấy một điểm A tùy ý và vẽ $\underset{AB}{\rightarrow}$=$\underset{a}{\rightarrow}$,$\underset{BC}{\rightarrow}$=$\underset{b}{\rightarrow}$. Khi đó vectơ $\underset{AC}{\rightarrow}$ được gọi là tổng của hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ và được kí hiệu là $\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$ 

Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

HĐ2: 

$\underset{AB}{\rightarrow}$+$\underset{AD}{\rightarrow}$=$\underset{AB}{\rightarrow}$+$\underset{BC}{\rightarrow}$=$\underset{AC}{\rightarrow}$

Vậy $\underset{AB}{\rightarrow}$+$\underset{AD}{\rightarrow}$=$\underset{AC}{\rightarrow}$

Quy tắc ba điểm:

Với ba điểm bất kì A, B, C, ta có $\underset{AB}{\rightarrow}$+$\underset{BC}{\rightarrow}$=$\underset{AC}{\rightarrow}$

Quy tắc hình bình hành:

Nếu ABCD là một hình bình hành thì $\underset{AB}{\rightarrow}$+$\underset{AD}{\rightarrow}$=$\underset{AC}{\rightarrow}$.

HĐ3:

a) $\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$=$\underset{AC}{\rightarrow}$

$\underset{b}{\rightarrow}$+$\underset{a}{\rightarrow}$=$\underset{AC}{\rightarrow}$

b) ($\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$)+$\underset{c}{\rightarrow}$=$\underset{AC}{\rightarrow}$+$\underset{CD}{\rightarrow}$=$\underset{AD}{\rightarrow}$

$\underset{a}{\rightarrow}$+($\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$)=$\underset{AB}{\rightarrow}$+$\underset{BD}{\rightarrow}$=$\underset{AD}{\rightarrow}$

Kết luận:

Với ba vectơ $\underset{a}{\rightarrow}$,$\underset{b}{\rightarrow}$,ctùy ý:

- Tính chất giao hoán: $\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$=$\underset{b}{\rightarrow}$+$\underset{a}{\rightarrow}$;

- Tính chất kết hợp: 

($\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$)+$\underset{c}{\rightarrow}$=$\underset{a}{\rightarrow}$+($\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$)

- Tính chất của vectơ-không: $\underset{a}{\rightarrow}$+$\underset{0}{\rightarrow}$=$\underset{0}{\rightarrow}$+$\underset{a}{\rightarrow}$=$\underset{a}{\rightarrow}$.

Chú ý: Do các vectơ ($\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$)+$\underset{c}{\rightarrow}$ và $\underset{a}{\rightarrow}$+($\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$) bằng nhau, nên ta còn viết chúng dưới dạng $\underset{a}{\rightarrow}$+$\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$ và gọi là tổng của ba vectơ $\underset{a}{\rightarrow}$,$\underset{b}{\rightarrow}$,$\underset{c}{\rightarrow}$. Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng các dấu ngoặc.

Ví dụ 1 (SGK – tr52)

Luyện tập 1: 

Do ABCD là hình thoi có $\widehat{BAD}$=120$^{\circ}$ nên các tam giác ABC, ADC là các tam giác đều. Do đó CA = CB = CD = 1. (1)

+ Tính độ dài của vectơ $\underset{CB}{\rightarrow}$+$\underset{CD}{\rightarrow}$:

Theo quy tắc hình bình hành, ta có:

$\underset{CB}{\rightarrow}$+$\underset{CD}{\rightarrow}$=$\underset{CA}{\rightarrow}$.

$\underset{CB}{\rightarrow}$+$\underset{CD}{\rightarrow}$=$\underset{CA}{\rightarrow}$=1.

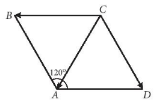
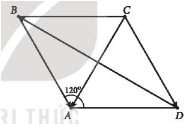
+ Tính độ dài của vectơ $\underset{DB}{\rightarrow}$+$\underset{CD}{\rightarrow}$+$\underset{BA}{\rightarrow}$:

Do tính giao hoán và tính kết hợp của phép cộng vectơ, nên:

$\underset{DB}{\rightarrow}$+$\underset{CD}{\rightarrow}$+$\underset{BA}{\rightarrow}$=$\underset{CD}{\rightarrow}$+$\underset{DB}{\rightarrow}$+$\underset{BA}{\rightarrow}$=($\underset{CD}{\rightarrow}$+$\underset{DB}{\rightarrow}$)+$\underset{BA}{\rightarrow}$=$\underset{CB}{\rightarrow}$+$\underset{BA}{\rightarrow}$=$\underset{CA}{\rightarrow}$

|$\underset{DB}{\rightarrow}$+$\underset{CD}{\rightarrow}$+$\underset{BA}{\rightarrow}$|=|$\underset{CA}{\rightarrow}$|=1.

2. HIỆU CỦA HAI VECTƠ

HĐ4: 

Hai lực cân bằng là hai lực mạnh như nhau, có cùng phương nhưng ngược chiều, tác dụng vào cùng một vật.

Hai vectơ sẽ ngược hướng nhau, điểm đầu của vectơ này là điểm cuối của vectơ kia và có độ dài bằng nhau.

Định nghĩa:

- Vectơ có cùng độ dài và ngược hướng với vectơ $\underset{a}{\rightarrow}$ được gọi là vectơ đối của vectơ $\underset{a}{\rightarrow}$. Vectơ đối của $\underset{a}{\rightarrow}$ được kí hiệu là -$\underset{a}{\rightarrow}$.

- Vectơ $\underset{0}{\rightarrow}$ được coi là vectơ đối của chính nó.

Chú ý: Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng $\underset{0}{\rightarrow}$.

Định nghĩa:

Vectơ $\underset{a}{\rightarrow}$+(-$\underset{b}{\rightarrow}$) được gọi là hiệu của hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ và được kí hiệu là $\underset{a}{\rightarrow}$-$\underset{b}{\rightarrow}$. Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

Chú ý:

Nếu $\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$=$\underset{a}{\rightarrow}$ thì $\underset{a}{\rightarrow}$-$\underset{b}{\rightarrow}$=$\underset{c}{\rightarrow}$

Quy tắc hiệu:

Với ba điểm O, M, N ta có $\underset{MN}{\rightarrow}$=$\underset{ON}{\rightarrow}$-$\underset{OM}{\rightarrow}$

Ví dụ 2 (SGK – tr53)

Ví dụ 3 (SGK – tr53)

Chú ý:

- Nếu I là trung điểm của đoạn thẳng AB thì $\underset{IA}{\rightarrow}$+$\underset{IB}{\rightarrow}$=0.

- Nếu G là trọng tâm tam giác ABC thì $\underset{GA}{\rightarrow}$+$\underset{GB}{\rightarrow}$+$\underset{GC}{\rightarrow}$=0

Luyện tập 2:

Cách 1: Sử dụng quy tắc hình bình hành

Lấy K và L lần lượt đối xứng với O qua M và N. Khi đó các tứ giác AOBK, CODL là các hình bình hành.

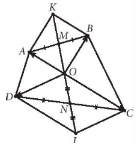
Hơn nữa, do O là trung điểm của MN nên

OK = 2OM = 2ON = OL, do đó O cũng là trung điểm của KL. Suy ra $\underset{OK}{\rightarrow}$+$\underset{OL}{\rightarrow}$=$\underset{0}{\rightarrow}$.

Từ đó suy ra:

$\underset{OA}{\rightarrow}$+$\underset{OB}{\rightarrow}$+$\underset{OC}{\rightarrow}$+$\underset{OD}{\rightarrow}$=($\underset{OA}{\rightarrow}$+$\underset{OB}{\rightarrow}$)+($\underset{OC}{\rightarrow}$+$\underset{OD}{\rightarrow}$)=$\underset{OK}{\rightarrow}$+$\underset{OL}{\rightarrow}$=$\underset{0}{\rightarrow}$.

Cách 2:

Do M là trung điểm của AB nên ta có: $\underset{MA}{\rightarrow}$.+$\underset{MB}{\rightarrow}$.=$\underset{0}{\rightarrow}$.

=> $\underset{OA}{\rightarrow}$.-$\underset{OM}{\rightarrow}$.+$\underset{OB}{\rightarrow}$.-$\underset{OM}{\rightarrow}$.=$\underset{0}{\rightarrow}$.

Hay $\underset{OA}{\rightarrow}$.+$\underset{OB}{\rightarrow}$.=$\underset{OM}{\rightarrow}$.+$\underset{OM}{\rightarrow}$.

Tương tự ta có: $\underset{OC}{\rightarrow}$.+$\underset{OD}{\rightarrow}$.=$\underset{ON}{\rightarrow}$.+$\underset{ON}{\rightarrow}$.

Từ đó suy ra:

$\underset{OA}{\rightarrow}$+$\underset{OB}{\rightarrow}$+$\underset{OC}{\rightarrow}$+$\underset{OD}{\rightarrow}$=$\underset{OM}{\rightarrow}$.+$\underset{OM}{\rightarrow}$+$\underset{ON}{\rightarrow}$.+$\underset{ON}{\rightarrow}$=$\underset{0}{\rightarrow}$.

Chú ý:

Phép cộng vectơ tương ứng với các quy tắc tổng hợp lực, tổng hợp vận tốc:

- Nếu hai lực cùng tác động vào chất điểm A và được biểu diễn bởi các vectơ $\underset{u_{1}}{\rightarrow}$,$\underset{u_{2}}{\rightarrow}$ thì hợp lực tác động vào A được biểu diễn bởi vectơ $\underset{u_{1}}{\rightarrow}$+$\underset{u_{2}}{\rightarrow}$.

- Nếu một con thuyền di chuyển trên sông với vận tốc riêng (vận tốc so với dòng nước) được biểu diễn bởi vectơ $\underset{v_{r}}{\rightarrow}$ và vận tốc của dòng nước (so với bờ) được biểu diễn bởi vectơ $\underset{v_{n}}{\rightarrow}$ thì vận tốc thực tế của thuyền (so với bờ) được biểu diễn bởi vectơ $\underset{v_{r}}{\rightarrow}$+$\underset{v_{n}}{\rightarrow}$.

Ví dụ 4: Giải bài toán trong tình huống mở đầu

Vận dụng:

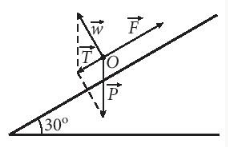
Lực tổng hợp của trọng lực $\underset{P}{\rightarrow}$ và phản lực $\underset{w}{\rightarrow}$ là lực $\underset{T}{\rightarrow}$ theo phương dốc, hướng từ đỉnh dốc xuống chân dốc, có độ lớn bằng |$\underset{P}{\rightarrow}$|.sin 30$^{\circ}$=11074 (N). Bởi vậy, để kéo được pháo lên dốc, lực kéo $\underset{F}{\rightarrow}$cần phải có độ lớn lớn hơn độ lớn của lực $\underset{T}{\rightarrow}$. Và do đó $\underset{F}{\rightarrow}$>$\underset{T}{\rightarrow}$=11074 (N).

Do $\frac{11074}{100}$=110,74 nên nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu 111 người để kéo pháo lên dốc.