Giải bài 4.7 bài tổng và hiệu của hai vectơ

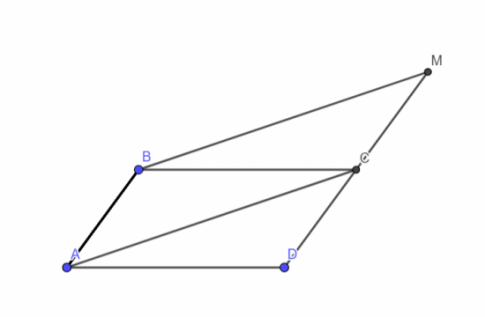
$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành)

Suy ra điểm M phải thỏa mãn $\overrightarrow{AC} = \overrightarrow{BM}$, hay ABMC là hình bình hành.

Ta có: ABMC là hình bình hành nên $\overrightarrow{AB} = \overrightarrow{CM}$

mà: $\overrightarrow{AB} = -\overrightarrow{CD}$ (hình bình hành ABCD)

Nên $\overrightarrow{CD} = -\overrightarrow{CM}$