Giải bài 4.14 bài tích của một vectơ với một số
Bài tập 4.14. Cho tam giác ABC
a. Hãy xác định điểm M để $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$
b. Chứng minh rằng với mọi điểm O, ta có $\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=4\overrightarrow{OM}$.
a. $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$
$\overrightarrow{MC}+\overrightarrow{CA}+\overrightarrow{MC}+\overrightarrow{CB}+2\overrightarrow{MC}=\overrightarrow{0}$
Suy ra: $4\overrightarrow{MC}=-\overrightarrow{CA}-\overrightarrow{CB}$
=$\overrightarrow{AC}+\overrightarrow{BC}$
Trên tia AC lấy điểm D sao cho C là trung điểm của AD, ta có:
$\overrightarrow{AC}+\overrightarrow{BC}$= $\overrightarrow{CD}+\overrightarrow{BC}$=$\overrightarrow{BD}$.
Vậy $\overrightarrow{MC}=\frac{1}{4}\overrightarrow{BD}$
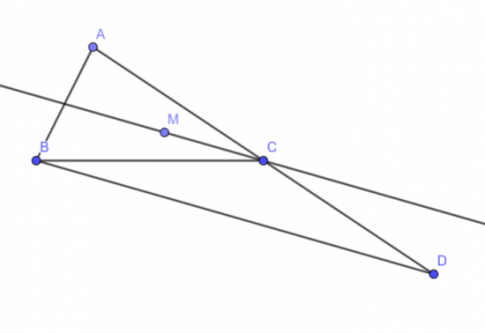
Cách vẽ M: Trên đường thẳng qua C và song song với BD lấy điểm M sao có $\overrightarrow{MC}=\frac{1}{4}\overrightarrow{BD}$ (như hình vẽ).
b. Theo a có: $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$
=> $\overrightarrow{OA}-\overrightarrow{OM}+\overrightarrow{OB}-\overrightarrow{OM}+2(\overrightarrow{OC}-\overrightarrow{OM})=\overrightarrow{0}$
Hay:$\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=4\overrightarrow{OM}$
Xem toàn bộ: Giải bài 9 Tích của một vectơ với một số

Bình luận