Bài giảng điện tử dạy thêm Toán 12 CTST Bài 3: Đường tiệm cận của đồ thị hàm số

Nội dung giáo án

CHÀO MỪNG CÁC EM 

ĐẾN VỚI BÀI HỌC MÔN TOÁN!

KHỞI ĐỘNG

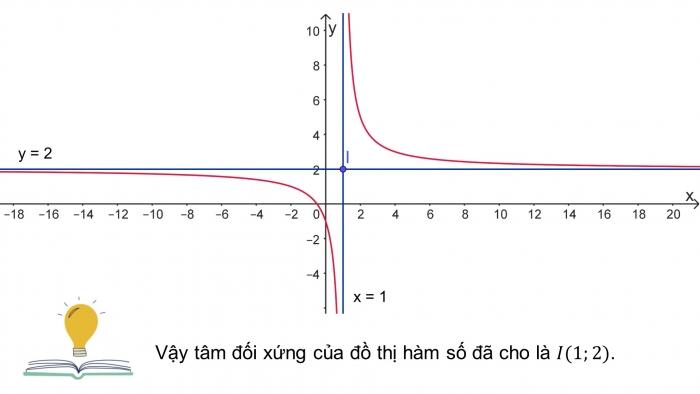
Tâm đối xứng của đồ thị hàm số có tọa độ là gì?

Giải

Tập xác định:

• nên là đường tiệm cận đứng của đồ thị hàm số đã cho.
• nên là đường tiệm cận ngang của đồ thị hàm số đã cho.

Vậy tâm đối xứng của đồ thị hàm số đã cho là .

BÀI 3: ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

I. HỆ THỐNG KIẾN THỨC

Yêu cầu:

Nêu khái niệm đường tiệm cận đứng, đường tiệm cận ngang và đường tiệm cận xiên của đồ thị hàm số.

1.

ĐƯỜNG TIỆM CẬN ĐỨNG

Đường thẳng được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số nếu ít nhất một trong các điều kiện sau thỏa mãn:

, 

.

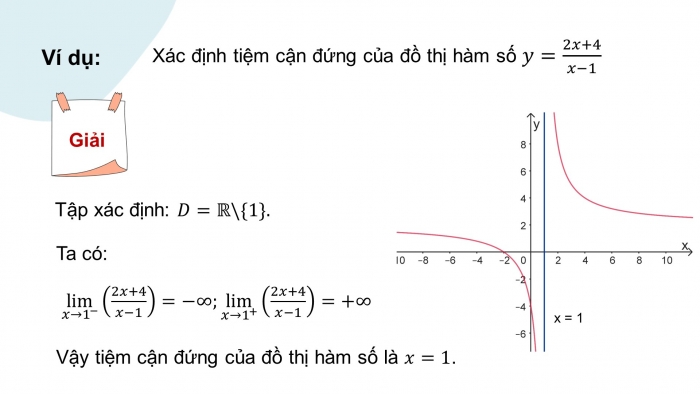
Ví dụ: 

Xác định tiệm cận đứng của đồ thị hàm số

Giải

Tập xác định:

Ta có:

Vậy tiệm cận đứng của đồ thị hàm số là .

2.

ĐƯỜNG TIỆM CẬN NGANG

Đường thẳng được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số nếu:

hoặc           

Ví dụ: Tìm đường tiệm cận ngang của đồ thị hàm số

Giải

Tập xác định:

Ta có:

và

Vậy đồ thị hàm số có tiệm cận ngang là đường thẳng có phương trình .

3.

ĐƯỜNG TIỆM CẬN XIÊN

Đường thẳng được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số nếu:

hoặc       .

Ví dụ: 

Chứng minh đường thẳng là một đường tiệm cận xiên của đồ thị hàm số .

Giải

Tập xác định:

Ta có:       

Vậy đường thẳng là một đường tiệm cận xiên của đồ thị hàm số đã cho.

Đồ thị hàm số có tiệm cận đứng và tiệm cận xiên

II. 

LUYỆN TẬP, VẬN DỤNG

DẠNG 1:

Xác định đường tiệm cận thông qua bảng biến thiên, đồ thị

Phương pháp giải:

• Đường thẳng được gọi là một tiệm cận đứng của đồ thị hàm số nếu ít nhất một trong các điều kiện sau thỏa mãn:

,

• Đường thẳng được gọi là một tiệm cận ngang của đồ thị hàm số nếu hoặc .

Bài 1:

Cho hàm số có bảng biến thiên như sau:

Xác định đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.

Giải

Ta có:

• và nên đồ thị hàm số có 2 tiệm cận ngang là các đường thẳng có phương trình và .
• nên hàm số có một tiệm cận đứng là đường thẳng có phương trình .

Bài 2:

Cho hàm số có bảng biến thiên như sau:

Xác định đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.

Giải

Ta có: 

suy ra là tiệm cận đứng của đồ thị hàm số.

suy ra là tiệm cận đứng của đồ thị hàm số.

suy ra là tiệm cận ngang của đồ thị hàm số.

Bài 3:

Cho hàm số có đồ thị hàm số như hình bên dưới. Hãy xác định các đường tiệm cận của đồ thị hàm số.

Giải

Từ đồ thị ta thấy:

• Đường tiệm cận ngang của đồ thị hàm số là
• Đường tiệm cận đứng của đồ thị hàm số là .

Bài 4:

Cho hàm số với và có bảng biến thiên như sau:

Tính giá trị của .

Giải

Từ bảng biến thiên ta có:

• nên đường tiệm cận ngang của đồ thị hàm số là suy ra .
• nên đường tiệm cận đứng của đồ thị hàm số là suy ra .

Vậy

DẠNG 2:

Xác định đường tiệm cận của đồ thị hàm số cho trước

--------------- Còn tiếp ---------------