Bài giảng điện tử dạy thêm Toán 12 CTST Bài 1: Vectơ và các phép toán trong không gian

Nội dung giáo án

CHÀO MỪNG CÁC EM 
ĐẾN VỚI BUỔI HỌC HÔM NAY!

KHỞI ĐỘNG

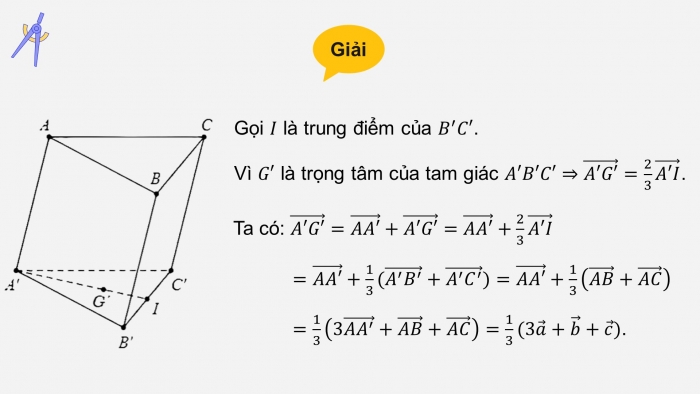
Cho hình lăng trụ . Đặt . Gọi là trọng tâm của tam giác . Biểu diễn vectơ theo các vectơ .

Giải

Gọi là trung điểm của .

Vì là trọng tâm của tam giác .

Ta có:

           .

CHƯƠNG 2: VECTƠ VÀ HỆ TỌA ĐỘ TRONG KHÔNG GIAN

BÀI 1: VECTƠ VÀ CÁC PHÉP TOÁN TRONG KHÔNG GIAN

I.

HỆ THỐNG KIẾN THỨC

Nhắc lại khái niệm vectơ trong không gian.

  1. Vectơ trong không gian

Vectơ trong không gian là một đoạn thẳng có hướng.

Chú ý:

• Kí hiệu chỉ vectơ có điểm đầu , điểm cuối .
• Nếu không cần chỉ rõ điểm đầu và điểm cuối thì vectơ còn được kí hiệu là
• Trong không gian, các khái niệm có liên quan đến vectơ như giá của vectơ; độ dài của vectơ; hai vectơ cùng phương, cùng hướng, ngược hướng, bằng nhau, đối nhau; vectơ – không được định nghĩa tương tự như trong mặt phẳng.

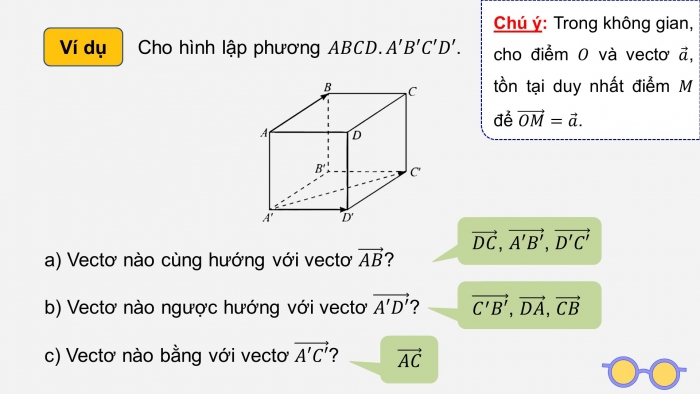
Ví dụ

Cho hình lập phương .

Chú ý: Trong không gian, cho điểm và vectơ , tồn tại duy nhất điểm để .

a) Vectơ nào cùng hướng với vectơ ?

b) Vectơ nào ngược hướng với vectơ ?

c) Vectơ nào bằng với vectơ ?

Nêu các quy tắc tổng, hiệu của hai vectơ, quy tắc hình bình hành, quy tắc hình hộp.

    2. Tổng và hiệu của hai vectơ

Tổng của hai vectơ:

• Trong không gian, cho hai vectơ . Lấy điểm bất kì và hai điểm sao cho , . Ta gọi là tổng của hai vectơ và , kí hiệu .
• Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

NHẬN XÉT

Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng.

Tính chất giao hoán:

Tính chất kết hợp:

Với mọi vectơ , ta luôn có: .

Quy tắc hình bình hành:

Quy tắc ba điểm, quy tắc hình bình hành vẫn đúng với các vectơ trong không gian.

• Với ba điểm ta có:
• Nếu là hình bình hành thì ta có:

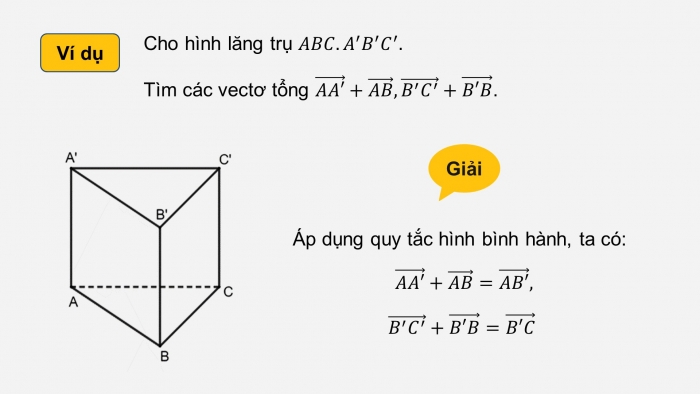
Ví dụ

Cho hình lăng trụ

Tìm các vectơ tổng .

Giải

Áp dụng quy tắc hình bình hành, ta có:

Quy tắc hình hộp:

Cho hình hộp . Ta có:

Ví dụ

Cho hình hộp chữ nhật . Tìm vectơ ?

Giải

Áp dụng quy tắc hình hộp, ta có:

Hiệu của hai vectơ:

Trong không gian, cho hai vectơ . Ta gọi là hiệu của hai vectơ và , kí hiệu .

Quy tắc hiệu: Trong không gian, với ba điểm ta có:

Ví dụ

Cho hình chóp có đáy là hình bình hành. Tìm vectơ hiệu .

Giải

Do là hình bình hành nên ta có:

Khi đó:

Nhắc lại công thức tính tích của một số với một vectơ trong không gian.

    3. Tích của một số với một vectơ

• Trong không gian, cho số thực và vectơ .
• Tích của số với vectơ là một vectơ, kí hiệu , cùng hướng với nếu , ngược hướng với nếu và có độ dài bằng .
• Phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ.
• Quy ước: và .

Ví dụ

Cho tứ diện . Gọi lần lượt là trung điểm của . Cho là trung điểm của . Chứng minh rằng: 

Với mọi điểm trong không gian.

Giải

Ta có: 

Vì là trung điểm của nên

      là trung điểm của nên

Mà là trung điểm của nên .

 .

Công thức tính tích vô hướng của hai vectơ là gì? Công thức tính góc giữa hai vectơ trong không gian?

    4. Tích vô hướng của hai vectơ

Góc giữa hai vectơ trong không gian

Nhận xét:

Trong không gian, cho và là hai vectơ khác . Lấy một điểm bất kì, gọi và là hai điểm sao cho . Khi đó, ta gọi là góc giữa hai vectơ và , kí hiệu .

• .
• Nếu thì ta nói và vuông góc với nhau, kí hiệu .

Tích vô hướng của hai vectơ

Trong không gian, cho hai vectơ và khác .

Tích vô hướng của hai vectơ và là một số, kí hiệu , được xác định bởi công thức

Ví dụ

Cho tứ diện có các cạnh , đôi một vuông góc và . Gọi là trung điểm của cạnh . Tính góc giữa hai vectơ và .

Giải

Ta có:

Mặt khác:

Vì đôi một vuông góc và nên và . 

Do đó: . 

   Vậy .

II.

LUYỆN TẬP, VẬN DỤNG

--------------- Còn tiếp ---------------