Bài giảng điện tử dạy thêm Toán 12 CTST Bài 1: Tính đơn điệu và cực trị của hàm số

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC 

MÔN TOÁN!

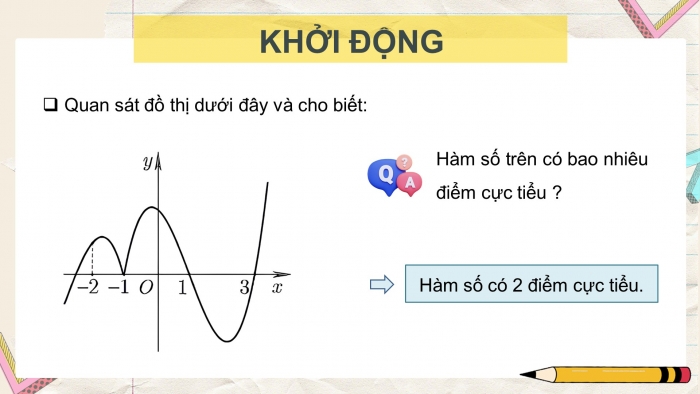
KHỞI ĐỘNG 

• Quan sát đồ thị dưới đây và cho biết:

Hàm số trên có bao nhiêu điểm cực tiểu ? 

Hàm số có 2 điểm cực tiểu.

CHỦ ĐỀ 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ

BÀI 1: TÍNH ĐƠN ĐIỆU VÀ 

CỰC TRỊ CỦA HÀM SỐ

HỆ THỐNG 

KIẾN THỨC

1. Tính đơn điệu của hàm số

Cho hàm số có đạo hàm trên .

Nếu với mọi thuộc thì hàm số đồng biến trên .

Nếu với mọi thuộc thì hàm số nghịch biến trên .

Chú ý: Khi xét tính đơn điệu của hàm số mà chưa cho khoảng , ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó.

Các bước thực hiện

Để xét tính đơn điệu của hàm số , ta thực hiện các bước sau:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm của hàm số. Tìm các điểm thuộc mà tại đó đạo hàm bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Xét dấu và lập bảng biến thiên.

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

• Ví dụ: Tìm các khoảng đơn điệu của hàm số .

Giải:

Tập xác định:

Ta có:

Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng và ,  nghịch biến trên các khoảng và .

Chú ý:

a) Nếu hàm số có đạo hàm trên , với mọi và chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên .

b) Nếu hàm số có đạo hàm trên , với mọi và chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên .

c) Nếu với mọi thì hàm số không đổi trên .

Giải:

Hàm số đã cho có tập xác định

Bảng biến thiên của hàm số như sau:

Vậy hàm số nghịch biến trên và .

2. Cực trị của hàm số

Khái niệm: Cho hàm số xác định trên tập hợp và .

• Nếu tồn tại một khoảng chứa điểm và sao cho với mọi thì được gọi là một điểm cực đại, được gọi là giá trị cực đại của hàm số , kí hiệu .
• Nếu tồn tại một khoảng chứa điểm và sao cho với mọi thì được gọi là một điểm cực tiểu, được gọi là giá trị cực tiểu của hàm số , kí hiệu .

Chú ý:

a) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (còn gọi là cực trị) của hàm số.

b) Nếu là một cực trị (điểm cực trị, điểm cực tiểu) của hàm số thì ta cũng nói hàm số đạt cực trị (cực đại, cực tiểu) tại .

c) Hàm số có thể đạt cực đại và cực tiểu tại nhiều điểm trên .

d) Nếu là điểm cực trị của hàm số thì điểm là một điểm cực trị của đồ thị hàm số .

• Ví dụ: Dựa vào đồ thị dưới đây, chỉ ra các điểm cực trị của hàm số.

Giải:

• Xét khoảng chứa điểm , ta có với mọi và .

Vậy là điểm cực tiểu của hàm số.

• Xét khoảng chứa điểm ta có với mọi và .

Vậy là điểm cực đại của hàm số.

Định lí:

Giả sử hàm số liên tục trên khoảng chứa điểm và có đạo hàm trên các khoảng và . Khi đó:

a) Nếu với mọi và với mọi thì hàm số đạt cực tiểu tại điểm

b)  Nếu với mọi và với mọi thì hàm số đạt cực đại tại điểm

Nhận xét:

Để tìm cực trị của hàm số ta thực hiện các bước sau:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm của hàm số. Tìm các điểm thuộc mà tại đó đạo hàm bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Lập bảng biến thiên của hàm số.

Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số. 

Giải:

Tập xác định:

Ta có: hoặc

Bảng biến thiên:

Vậy hàm số đạt cực đại tại và đạt cực tiểu tại .

Chú ý:

a) Nếu và không đổi dấu khi qua điểm thì hàm số không có cực trị tại .

b) Nếu không đổi dấu trên khoảng thì không có cực trị trên khoảng đó.

LUYỆN 

TẬP

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Xét tính đơn điệu của hàm số cho bởi biểu thức.

Phương pháp giải: 

Để xét tính đơn điệu của hàm số , ta thực hiện các bước sau:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm của hàm số. Tìm các điểm thuộc mà tại đó đạo hàm bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Xét dấu và lập bảng biến thiên.

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Bài 1. Tìm các khoảng đơn điệu của các hàm số sau: a)

Giải:

Tập xác định:

Ta có: hoặc

Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng và ; hàm số nghịch biến trên khoảng .

Giải:

--------------- Còn tiếp ---------------