Giải mở đầu trang 52 sgk Toán 8 tập 2 CD

Gọi A,B là hai đầu mút của thanh sắt

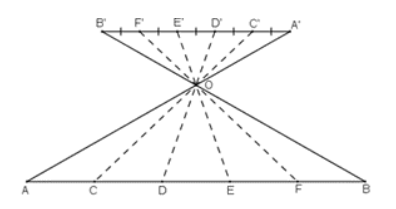
- Vẽ đoạn thẳng A'B' song song với AB, A'B' có độ dài 5 đơn vị.

- C', D', E', F' nằm trên A'B' sao cho A'C' = C'D' = D'E' = E'F' = F'B' = 1. Xác định giao điểm O của hai đoạn thẳng AA' và BB'. 

- Vẽ các đường thẳng OC', OD', OE', OF' cắt AB lần lượt tại C, D, E, F. 

- Theo hệ quả của định lý Thalès ta có: 

AC // A'C' (C $\in $ AB, C' $\in $ A'B') nên $\frac{AC}{A'C'}=\frac{OA}{OA'}=\frac{OC}{OC'}$ (1)

Tương tự ta có: $\frac{CD}{C'D'}=\frac{OC}{OC'}=\frac{OD}{OD'}$ (2)

$\frac{DE}{D'E'}=\frac{OD}{OD'}=\frac{OE}{OE'}$ (3)

$\frac{EF}{E'F'}=\frac{OE}{OE'}=\frac{OF}{OF'}$ (4)

$\frac{FB}{F'B'}=\frac{OF}{OF'}=\frac{OB}{OB'}$ (5)

Từ (1)(2)(3)(4)(5) suy ra: $\frac{AC}{A'C'}=\frac{CD}{C'D'}=\frac{DE}{D'E'}=\frac{EF}{E'F'}=\frac{FB}{F'B'}$.

Mà A'C' = C'D' = D'E' = E'F' = F'B' = 1

Do đó: AC = CD= DE = EF = FB. (đpcm)