Giải hoạt động 1 trang 47 chuyên đề toán 10 kết nối tri thức
1.HÌNH DẠNG CỦA HYPEBOL
Hoạt động 1: Trong mặt phẳng tọa độ cho hypebol có phương trình chính tắc
a, Hãy giải thích vì sao nếu điểm M(x0; y0) thuộc hypebol thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc hypebol (H.3.12).
b, Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c, Với điểm M(x0; y0) thuộc hypebol, hãy so sánh |x0| với a.
a, Nếu điểm M(x0; y0) thuộc hypebol thì ta có:
Ta có: 
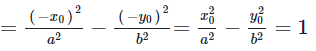
Nên các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc elip.
b, Gọi A là giao điểm của hypebol với trục hoành.
Vì A thuộc trục Ox nên toạ độ của A có dạng (xA; 0)
Mà A thuộc hypebol nên
Do đó hypebol cắt trục Ox tại hai điểm A1(–a; 0) và A2(a; 0).
Giả sử hypebol cắt trục tung tại B.
Vì B thuộc trục Oy nên toạ độ của B có dạng (0; yB).
Mà B thuộc hypebol nên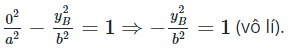 
Vậy hypebol không cắt trục tung.
c, M(x0; y0) thuộc hypebol nên ta có 
Xem toàn bộ: Giải chuyên đề toán 10 kết nối bài 6 Hypebol
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận