Giải câu 17 bài tập cuối chương IX

Chọn hệ tọa độ như hình vẽ:

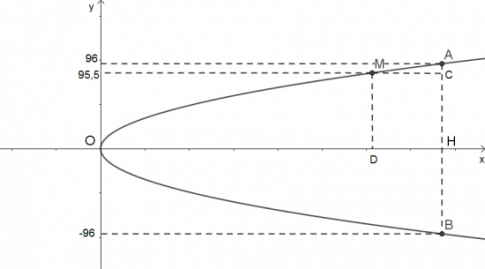
Gọi phương trình parabol là $y^{2} = 2px$.

Gọi chiều cao của cổng là OH = h.

Khoảng cách giữa hai chân cổng là AB = 192 $\Rightarrow$ AH = 96 $\Rightarrow$ điểm A có tọa độ (h; 96).

Ta có: AC = 0,5; DH = MC = 2 $\Rightarrow$ điểm M có tọa độ (h - 2; 95,5).

Vì A và M thuộc parabol (P) nên ta có hệ phương trình:

$\left\{\begin{matrix}96^{2} = 2ph\\95,5^{2} = 2p(h - 2) \end{matrix}\right.$ $\Rightarrow$ $\frac{96^{2}}{95,5^{2}}$ = $\frac{h}{h - 2}$ $\Rightarrow$ h = $\frac{2. 96^{2}}{96^{2} - 95,5^{2}}$ $\approx$ 192,5 (m)

Vậy chiều cao của cổng khoảng 192,5 m.