Giải bài tập 6.61 trang 27 SBT toán 10 tập 2 kết nối

Đặt AM = x (0 < x < 13).

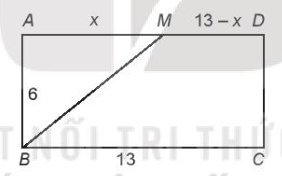
Xét tam giác ABM vuông tại A, áp dụng định lí Pythagore ta có:

$AM^{2} + AB^{2}  = BM^{2}$

$=> BM=\sqrt{AM^{2}+AB^{2}}=\sqrt{36+x^{2}}$ và MD =13 – x.

Theo giả thiết ta có: BM = 2MD

=> $\sqrt{36+x^{2}}=2(13-x)<=>\sqrt{36+x^{2}}=26-2x$ (*)

Bình phương hai vế của (*) ta có:

$36 + x^{2} = 26^{2} – 104x + 4x^{2}$

$⇔ 3x^{2} – 104x + 640 = 0$

⇔ x = 8 (thỏa mãn) hoặc x = $\frac{80}{3}$ > 13 (loại)

Vậy AM = 8 cm hay điểm M nằm trên cạnh AD sao cho AM = 8 cm thì thỏa mãn yêu cầu bài toán.