Giải bài tập 4.65 trang 70 SBT toán 10 tập 1 kết nối
Bài tập 4.65. Cho hình thang vuông ABCD có $\widehat{DAB} = \widehat{ABC} = 90^{o}$, BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.
a) Hãy biểu thị các vectơ $\overrightarrow{CM}, \overrightarrow{CD}$ theo hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AD}$.
b) Gọi N là trung điểm CD, G là trọng tâm tam giác MCD và I là điểm thuộc cạnh CD sao cho 9IC = 5ID. Chứng minh rằng A, G, I thẳng hàng.
c) Tính độ dài các đoạn thẳng AI và BI.
Trả lời:
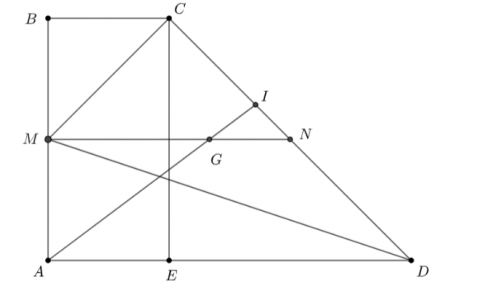
a) Có BC = 2 và AD =1
BC // AD (ABCD là hình thang vuông tại A, B)
$\Rightarrow \overrightarrow{BC} = \frac{1}{3}\overrightarrow{AD}$
Có $\overrightarrow{CM} = \overrightarrow{BM} - \overrightarrow{BC} = \frac{1}{2}\overrightarrow{AB} - \frac{1}{3}\overrightarrow{AD}$
Có $\overrightarrow{CD} = \overrightarrow{CB} + \overrightarrow{BA} + \overrightarrow{AD} = -\overrightarrow{BC} - \overrightarrow{AB} + \overrightarrow{AD} = -\frac{1}{3}\overrightarrow{AD} - \overrightarrow{AB} + \overrightarrow{AD} = \frac{2}{3}\overrightarrow{AD} - \overrightarrow{AB}$
b) Có G là trọng tâm tam giác MCD
$\Rightarrow 3\overrightarrow{AG} = \overrightarrow{AM} + \overrightarrow{AC} + \overrightarrow{AD} = \frac{1}{2}\overrightarrow{AB} + (\overrightarrow{AB} + \overrightarrow{BC}) + \overrightarrow{AD} = \frac{2}{3}\overrightarrow{AB} + \frac{4}{3}\overrightarrow{AD}$
$\Rightarrow 6. 3\overrightarrow{AG} = 18\overrightarrow{AG} = 9\overrightarrow{AB} + 8\overrightarrow{AD}$ (1)
Có 9IC = 5ID
$\Rightarrow 9\overrightarrow{IC} + 5\overrightarrow{ID} = 0$
$\Leftrightarrow 9(\overrightarrow{AC} - \overrightarrow{AI}) + 5(\overrightarrow{AD} - \overrightarrow{AI}) = \overrightarrow{0}$
$\Leftrightarrow 14\overrightarrow{AI} = 9\overrightarrow{AC} + 5\overrightarrow{AD}$
$\Leftrightarrow 14\overrightarrow{AI} = 9(\overrightarrow{AB} + \overrightarrow{BC}) + 5\overrightarrow{AD} = 9\overrightarrow{AB} + 9.\frac{1}{3}\overrightarrow{AD} + 5\overrightarrow{AD}$
$\Leftrightarrow 14\overrightarrow{AI} = 9\overrightarrow{AB} + 8\overrightarrow{AD}$ (2)
Từ (1) và (2) suy ra $18\overrightarrow{AG} = 14\overrightarrow{AI}$
$\Rightarrow \overrightarrow{AG}$ và $\overrightarrow{AI}$ cùng hướng
Vậy ba điểm A, G, I thẳng hàng
c) Có $14\overrightarrow{AI} = 9\overrightarrow{AB} + 8\overrightarrow{AD}$ (chứng minh câu b)
$\Rightarrow (14\overrightarrow{AI})^{2} = (9\overrightarrow{AB} + 8\overrightarrow{AD})^{2} = 81\overrightarrow{AB}^{2} + 144\overrightarrow{AB} . \overrightarrow{AD} + 64\overrightarrow{AD}^{2}$
$\Rightarrow 194\overrightarrow{AI}^{2} = 81\overrightarrow{AB}^{2} + 64\overrightarrow{AD}^{2} = 81 . 4 + 64 . 9 = 900$
$\Rightarrow AI^{2} = \frac{900}{196}$
Vậy AI = $\frac{15}{7}$
Có $\overrightarrow{BI} = \overrightarrow{AI} - \overrightarrow{AB} = \frac{9}{14}\overrightarrow{AB} + \frac{4}{7}\overrightarrow{AD} - \overrightarrow{AB} = \frac{4}{7}\overrightarrow{AD} - \frac{5}{14}\overrightarrow{AB}$
$\Rightarrow BI^{2} = (\frac{4}{7}\overrightarrow{AD} - \frac{5}{14}\overrightarrow{AB})^{2} = \frac{16}{49}\overrightarrow{AD}^{2} - \frac{20}{49}\overrightarrow{AD}.\overrightarrow{AB} + \frac{25}{196}\overrightarrow{AB}^{2}$
$\Rightarrow BI^{2} = \frac{16}{49}\overrightarrow{AD}^{2} + \frac{25}{196}\overrightarrow{AB}^{2} = \frac{16}{49}. 9 + \frac{25}{196}. 4 = \frac{169}{49}$
Vậy BI = $\frac{13}{7}$
Xem toàn bộ: Giải SBT toán 10 kết nối Bài tập cuối chương IV

Bình luận