Giải bài tập 4.41 trang 67 SBT toán 10 tập 1 kết nối
Bài tập 4.41. Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lây từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ $\overrightarrow{AK}$?
A.2. B. 6.
C.4. D. 8.
Trả lời: Chọn đáp án: B. 6.
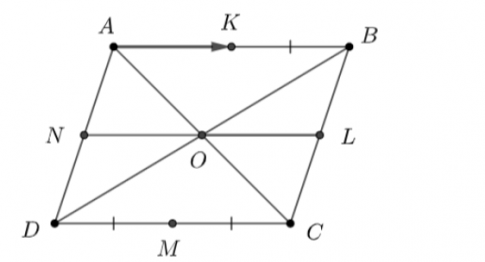
Hình bình hành ABCD có AB = CD
Có K, M lần lượt là trung điểm AB, CD nên ta có AK = KB = CM = DM (1)
Có NL là đường trung bình hình bình hành ABCD nên NL // AB hay AN // BL
Suy ra tứ giác ABLN là hình bình hành cho nên AB = NL
Có O là trung điểm NL, K là trung điểm AB, AB = NL
Suy ra AK = NO = OL = AB (2)
Từ (1) và (2) suy ra ÂK = KB = NO = OL = DM = MC
Mà KB, NO, OL, DM, MC song song với AK
Suy ra $\overrightarrow{AK} = \overrightarrow{KB} = \overrightarrow{NO} = \overrightarrow{OL} = \overrightarrow{DM} = \overrightarrow{MC}$
Xem toàn bộ: Giải SBT toán 10 kết nối Bài tập cuối chương IV

Bình luận