Giải bài tập 4.62 trang 70 SBT toán 10 tập 1 kết nối

Trả lời:

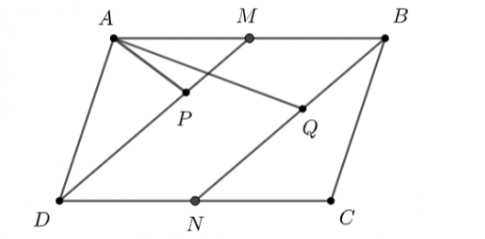
a) Có

$\overrightarrow{AP} = \overrightarrow{AD} + \overrightarrow{DP} = \overrightarrow{AD} + \frac{2}{3}\overrightarrow{DM} = \overrightarrow{AD} + \frac{2}{3}(\overrightarrow{AM} - \overrightarrow{AD}) = \frac{1}{3}\overrightarrow{AD} + \frac{2}{3}\overrightarrow{AM} = \frac{1}{3}\overrightarrow{AD} + \frac{2}{3} . \frac{1}{2}\overrightarrow{AB} = \frac{1}{3}\overrightarrow{u} + \frac{1}{3}\overrightarrow{v}$

Có BQ = xQN

$\Rightarrow \overrightarrow{BQ} = x\overrightarrow{QN}$

$\Leftrightarrow \overrightarrow{AQ} - \overrightarrow{AB} = x(\overrightarrow{AN} - \overrightarrow{AQ})$

$\Leftrightarrow (x + 1)\overrightarrow{AQ} = \overrightarrow{AB} x\overrightarrow{AN}$

$\Leftrightarrow (x + 1)\overrightarrow{AQ} = \overrightarrow{AB} + (\overrightarrow{AD} - \overrightarrow{DN}) = x\overrightarrow{AD} + \overrightarrow{AB} + x.\frac{1}{2}\overrightarrow{AB}$

$\Leftrightarrow (x + 1)\overrightarrow{AQ} = x\overrightarrow{AD} + (\frac{1}{2}x + 1)\overrightarrow{AB}$

$\Leftrightarrow (x + 1)\overrightarrow{AQ} = x\overrightarrow{u} + (\frac{1}{2}x + 1)\overrightarrow{v}$

$\Leftrightarrow \overrightarrow{AQ} = \frac{x + 2}{2(x + 1)}\overrightarrow{u} + \frac{x}{x + 1}\overrightarrow{v}$

b) A, P, Q thằng hàng $\Leftrightarrow \overrightarrow{AP} và  \overrightarrow{AQ}$ cùng phương

$\Leftrightarrow \frac{x + 2}{2(x + 1)} : \frac{2}{3} = \frac{x}{x + 1} : \frac{2}{3}$ với x $\neq$ -1

$\Leftrightarrow \frac{x + 2}{2} = x$

$\Leftrightarrow x = 2$ thỏa mãn điều kiện