Giải bài tập 4.56 trang 69 SBT toán 10 tập 1 kết nối

Trả lời: Chọn đáp án: A. $\frac{5}{12}$

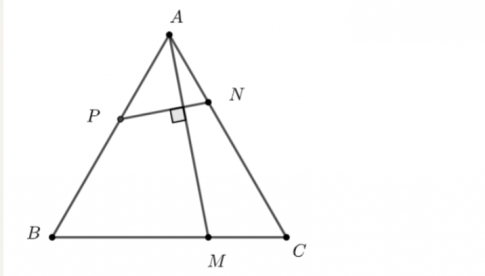
Đặt AP = x (0 < x < 1)

Có $\overrightarrow{PN} = \overrightarrow{PA} + \overrightarrow{AN} = \frac{1}{3}\overrightarrow{AC} -x\overrightarrow{AB}$

Có $\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{BM} = \overrightarrow{AB} + \frac{2}{3}\overrightarrow{BC} = \frac{2}{3}(\overrightarrow{AC} - \overrightarrow{AB} = \frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}$

Có AM $\perp$ NP $\Rightarrow \overrightarrow{AM} . \overrightarrow{PN} = 0$

$\Leftrightarrow (\frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}) . (\frac{1}{3}\overrightarrow{AC} -x\overrightarrow{AB}) = 0$

$\Leftrightarrow \frac{1}{9}\overrightarrow{AB} . \overrightarrow{AC} - \frac{x}{3}\overrightarrow{AB}^{2} + \frac{1}{9}\overrightarrow{AC}^{2}  - \frac{2x}{3}\overrightarrow{AC} . \overrightarrow{AB} = 0$

$\Leftrightarrow \frac{1}{9} . \frac{1}{2} - \frac{x}{3} + \frac{2}{9} - \frac{2x}{3} . \frac{1}{2} = 0$

$\Leftrightarrow \frac{1}{18} - \frac{x}{3} + \frac{2}{9} - \frac{x}{3} = 0$

$\Leftrightarrow 1 - 6x + 4 - 6x = 0$

$\Leftrightarrow x = \frac{5}{12}$