Giải bài tập 4.28 trang 59 SBT toán 10 tập 1 kết nối

Trả lời: 

Chọn hệ trục tọa độ Oxy sao cho các đỉnh của hình hồ hình chữ nhật có các tọa độ là A(0; 0), B(200; 0), C(200; 180) và D(0; 180)

Gọi vị trí các cột điện được trồng là $C _{1}, C _{2}, C _{3}, C _{4}$

Vì vị trí cột điện thứ nhất $C _{1}$ nằm trên bờ AB và cách A một khoảng 20 m nên trong hệ trục tọa độ đã chọn, điểm $C _{1}$(20; 0)

Vị trí cột điện thứ tư nằm trên bờ CD và cách C một khoảng 30 m nên khoảng cách từ $C _{4}$ đến D là 170 m. Khi đó trong hệ trục tọa độ đã chọn, điểm $C _{4}$(170; 180)

Vì bốn cột điện được trồng liên tiếp nhau và cách đều trên một đường thẳng nên:

$C _{1}C _{2} = C _{2}C _{3} = C _{3}C _{4}$

$\Rightarrow C _{1}C _{2} = \frac{1}{3}C _{1}C _{4}$, $C _{1}C _{3} = \frac{2}{3}C _{1}C _{4}$

$\Rightarrow \overrightarrow{C_{1}C_{2}} = \frac{1}{3}\overrightarrow{C_{1}C_{4}}$, $\overrightarrow{C _{1}C _{3}} = \frac{2}{3}\overrightarrow{C _{1}C _{4}}$

Giả sử $C_{2}$ = (a; b), $C_{3}$ = (c; d) với $C_{1}$(20; 0), $C_{4}$(170; 180) ta có:

$\overrightarrow{C _{1}C _{4}} = (150; 180)$, $\overrightarrow{C _{1}C _{2}} = (a - 20; b)$, $\overrightarrow{C _{1}C _{3}} = (c - 20; y)$

$\overrightarrow{C _{1}C _{2}} = \frac{1}{3}\overrightarrow{C _{1}C _{4}} \Leftrightarrow$ $\Leftrightarrow$

Vậy $C _{2} = (70; 60)$

$\Rightarrow d(C _{2}; AB) = d(C _{2}; O _{c}) = |b| = 60$ (m)

$\Rightarrow d(C _{2}; AD) = d(C _{2}; O _{d}) = |a| = 70$ (m)

$\overrightarrow{C _{1}C _{3}} = \frac{2}{3}\overrightarrow{C _{1}C _{4}} \Leftrightarrow$$\Leftrightarrow$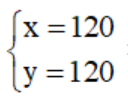

Vậy $C _{3} = (120; 120)$

$\Rightarrow d(C _{3}; AB) = d(C _{3}; O _{c}) = |d| = 120$ (m)

$\Rightarrow d(C _{3}; AD) = d(C _{3}; O _{d}) = |c| = 70$ (m)

Vậy khoảng cách từ cột điện thứ hai đến bờ AB là 60 m và đến bờ AD là 70 m và khoảng cách từ cột điện thứ ba đến bờ AB là 120 m và đến bờ AD là 120 m