Giải bài tập 4.24 trang 58 SBT toán 10 tập 1 kết nối

Trả lời:

Gọi P(a; 0) là điểm thuộc tia Ox.

Với M(–2; 1) và N(4; 5) ta có:

$\overrightarrow{PM}$ = (-2 - a; 1)

$\Rightarrow PM = |\overrightarrow{PM}| = \sqrt{(-2 - a)^{2} + 1^{2}}$

$\overrightarrow{PN}$ = (4 - a; 5)

$\Rightarrow PN = |\overrightarrow{PN}| = \sqrt{(4 - a)^{2} + 5^{2}}$

PM = PN $\Leftrightarrow \sqrt{(-2 - a)^{2} + 1^{2}} = \sqrt{(4 - a)^{2} + 5^{2}}$

$\Rightarrow (-2 - a)^{2} + 1^{2} = (4 - a)^{2} + 5^{2}$

$\Rightarrow 4 + 4a + a^{2} + 1 = 16 - 8a + a^{2} + 25$

$\Rightarrow 12a= 36$

$\Rightarrow a = 3$

b) Giả sử điểm Q có tọa độ là Q(x; y) với M(–2; 1), N(4; 5) và P(3; 0) ta có:

$\overrightarrow{MQ}$ = (x + 2; y - 1)

$\overrightarrow{PN}$ = (4 - 3; 5 - 0) = (1; 5)

$\Rightarrow 2\overrightarrow{PN}$ = (2; 10)

$\overrightarrow{MQ} = 2\overrightarrow{PN} \Leftrightarrow$ 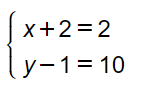$\Leftrightarrow$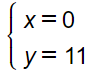

$\Rightarrow$ Q(0; 11)

c) Giả sử $R(x_{0}; y _{0})$ là điểm cần tìm với M(–2; 1) và N(4; 5) ta có:

$\overrightarrow{RM} = (-2 - x_{0}; 1 - y _{0})$

$\overrightarrow{RN} = (4 - x_{0}; 5 - y _{0})$

$\Rightarrow 2\overrightarrow{RN} = (8 - 2x_{0}; 10 - 2y _{0})$

$\Rightarrow \overrightarrow{RM} + 2\overrightarrow{RN} = (6 - 3x_{0}; 11 - 3y _{0})$

$\overrightarrow{RM} + 2\overrightarrow{RN} = \overrightarrow{0} \Leftrightarrow$ 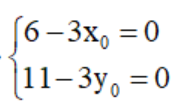$\Leftrightarrow$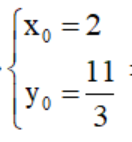

$\Rightarrow R (2; \frac{11}{3})$

Có P(3; 0), Q(0; 11), R(2; $\frac{11}{3}$)

$\Rightarrow \overrightarrow{PQ}$ = (-3; 11), $\overrightarrow{QR}$ = (2; $\frac{-22}{3}$)

Vậy $\overrightarrow{PQ}$ và $\overrightarrow{QR}$ cùng phương 

Do đó P, Q, R thẳng hàng