Giải bài tập 4 trang 13 chuyên đề toán 10 chân trời sáng tạo
4. Tìm phương trình của Parabol (P): y= $ax^2$ + bx + c (a ≠ 0), biết:
a) Parabol (P) có trục đối xứng x = 1 và đi qua hai điểm A(1; –4), B(2; –3);
b) Parabol (P) có đỉnh I và đi qua điểm M(–1; 3).
a) Theo đề bài ta có:
(P) có trục đối xứng x = 1, suy ra $\frac{b}{2}$= 1, suy ra 2a + b = 0 (1).
(P) đi qua điểm A(1; –4), suy ra –4 = a . $1^2$ + b . 1 + c hay a + b + c = –4 (2).
(P) đi qua điểm B(2; –3), suy ra –3 = a . $2^2$ + b . 2 + c hay 4a + 2b + c = –3 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
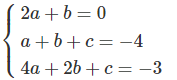
Giải hệ này ta được a = 1, b = –2, c = –3
Vậy phương trình của (P) là y = $x^2$ – 2x – 3.
b, Theo đề bài ta có:
(P) có có đỉnh I(1,2;3/2)
Suy ra : $\frac{b}{2}$=1/2 hay a+b=0(1)
Và $3/4$=$a(0,5)^2$+0,5b+c
Hay a+2b+4c=3(2)
(P) đi qua điểm M(–1; 3), suy ra 3 = a . (–1)^2 + b . (–1) + c hay a – b + c = 3 (3).
Từ (1), (2) và (3) ta có hệ phương trình:

Giải hệ này ta được a = 1, b = –1, c = 1.
Vậy phương trình của (P) là y = $x^2$ – x + 1.

Bình luận