Giải bài tập 3 trang 64 chuyên đề toán 10 chân trời sáng tạo
3. Viết phương trình của conic (C) trong mỗi trường hợp sau:
a) (C) có tiêu điểm F(8; 0), đường chuẩn Δ: x – 2 = 0 và tâm sai e = 2;
b) (C) có tiêu điểm F(–4; 0), đường chuẩn Δ:x+$\frac{25}{4}$=0
và tâm sai e=$\frac{4}{5}$
a) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có:
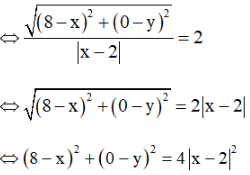
<=> (64-16x+$x^2$) + $y^2$ = 4($x^2$ -4x +4)
<=> 3$x^2$ -$y^2$ = 48
<=> $\frac{x^2}{16}$ - $\frac{y^2}{48}$ = 1
Vậy phương trình của conic đã cho là
$\frac{x^2}{16}$ - $\frac{y^2}{48}$ = 1
b, Gọi M(x; y) là điểm bất kì thuộc conic.
Khi đó, ta có: ![]()

<=> 16 + 8x + $x^2$ + $y^2$ = $\frac{16}{25}$$x^2$ + 8x + 25
<=> $\frac{9}{25}$$x^2$ + $y^2$ = 9
$\frac{x^2}{25}$ - $\frac{y^2}{9}$ = 1
Vậy phương trình của conic đã cho là
$\frac{x^2}{25}$ - $\frac{y^2}{9}$ = 1

Bình luận