Giải bài 4.39 bài tập cuối chương IV

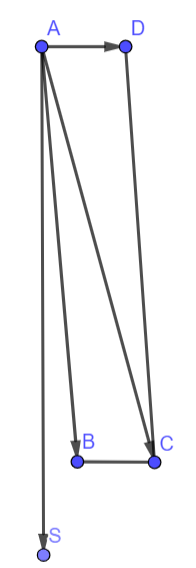
Gọi vecto $\overrightarrow{AD}$ là vecto vận tốc của dòng nước có độ lớn bằng 3 (theo hướng đông).

vecto $\overrightarrow{AC}$ là vecto vận tốc của cano, sao cho AC hợp với AS góc $15^{o}$ (do ca no chuyển động theo hướng S15^oE .

vecto $\overrightarrow{AB}$ là vecto vận tốc riêng của cano.

Ta có: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

AD = 3, AC = 20, ta tính AC.

Có góc $\widehat{SAC}=15^{o}\Rightarrow \widehat{CAD}=90^{o}-\widehat{SAC}=75^{o}$

Xét tam giác ADC, áp dụng định lí cosin ta có: $DC^{2}=AD^{2}+AC^{2}-2.AD.AC.cosDAC$

=> $DC\approx 19,4$

Mà ABCD là hình bình hành nên AB = DC = 19,4.

Vậy vận tốc riêng của cano là 19,4 km/h.