Câu hỏi tự luận mức độ vận dụng Toán 9 ctst bài hoạt động thực hành và trải nghiệm 1: Làm giác kế đo góc nâng đơn giản
3. VẬN DỤNG (3 câu)
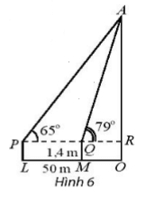
Câu 1: Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng ![]() người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng
người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng ![]() . Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m
. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m
Câu 2: Một học sinh sử dụng giác kế để đo góc nâng của một cột cờ. Khi mắt học sinh đặt vuông góc với mặt đĩa chia độ, số đo trên mặt đĩa chia độ là 30°. Góc nâng của cột cờ là?
Câu 3: Một học sinh dùng kế giác, đứng cách chân cột cờ 10m rồi chỉnh mặt thước ngắm cao bằng mắt của mình để xác định góc "nâng" (góc tạo bởi tia sáng đi thẳng từ đỉnh cột cờ với mắt tạo với phương nằm ngang). Khi đó, góc "nâng" đo được 31![]() . Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng 1,5m. Tính chiều cao cột cờ (kết quả làm tròn đến một chữ số thập phân).
. Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng 1,5m. Tính chiều cao cột cờ (kết quả làm tròn đến một chữ số thập phân).
3. VẬN DỤNG (3 câu)
Câu 1:
Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: ![]() = 79° và
= 79° và ![]() = 65°
= 65°
tan ![]() =
= ![]()
tan![]()
Ta có:
PQ = PR – QR = ![]()
=> h ≈ 183,9 (m)
Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).
Câu 2:
30![]()
Câu 3:
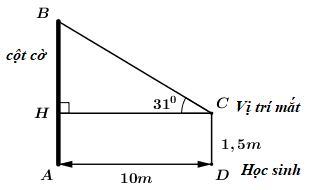
- Áp dụng định lý Pytago trong tam giác vuông AHB tính BH.
- Áp dụng hệ thức lượng trong tam giác vuông ABC tính BC: ![]()
Từ đó ta tính được AB = 7,5 (m).
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận