CHƯƠNG 2. CÁC HÌNH KHỐI TRONG THỰC TIỄN

BÀI 2. DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH CỦA HÌNH CHÓP TAM GIÁC ĐỀU, HÌNH CHÓP TỨ GIÁC ĐỀU

1. HÌNH CHÓP TAM GIÁC ĐỀU – HÌNH CHÓP TỨ GIÁC ĐỀU 

HĐKP:

a) Các mặt bên của Hình 1a, Hình 1b là hình chữ nhật.

Các mặt bên của Hình 1c, Hình 1d là hình tam giác.

b) Cả bốn hình (Hình 1a, 1b, 1c, 1d) đều có các cạnh bên bằng nhau.

+ Hình 1a và Hình 1c có đáy là tam giác đều.

Vậy Hình 1a và Hình 1c có các cạnh bên bằng nhau và đáy là hình tam giác đều.

c) Cả bốn hình (Hình 1a, 1b, 1c, 1d) đều có các cạnh bên bằng nhau.

+ Hình 1b và Hình 1d có đáy là hình vuông.

Vậy Hình 1b và Hình 1d có các cạnh bên bằng nhau và đáy là hình vuông.

• Hình chóp tam giác đều

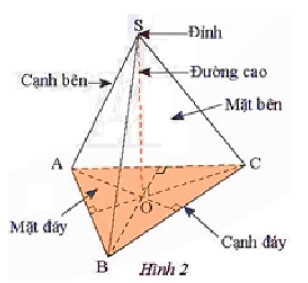
Hình S.ABC (Hình 2) là một hình chóp tam giác đều.

Trong hình này:

– S gọi là đỉnh.

– Mặt ABC là một tam giác đều và được gọi là mặt đáy (gọi tắt là đáy)

– Các đoạn thẳng SA, SB, SC bằng nhau và được gọi là các cạnh bên.

– Ba mặt SAB, SBC, SCAlà các tam giác cân đỉnh S bằng nhau và được gọi là ba mặt bên.

– Các đoạn thẳng AB, BC, CA được gọi là cạnh đáy.

– Gọi O là trọng tâm của mặt đáy, khi đó SO gọi là đường cao, độ dài SO gọi là chiều cao.

Thực hành 1. 

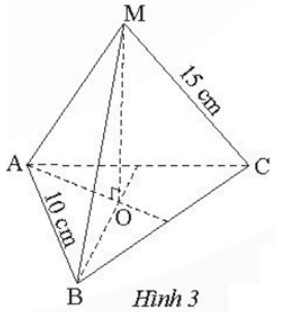
Hình chóp tam giác đều M.ABC ở Hình 3 có:

+ Các mặt bên: MAB, MBC, MAC;

+ Mặt đáy: ABC;

+ Đường cao: MO;

+ Độ dài cạnh bên: 15 cm (do các cạnh bên MA = MB = MC = 15 cm);

+ Độ dài cạnh đáy: 10 cm (do các cạnh đáy AB = BC = CA = 10 cm).

• Hình chóp tứ giác đều

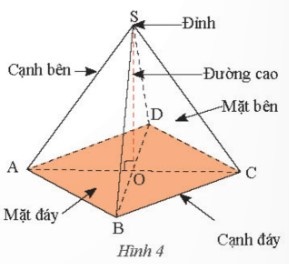
Hình S.ABCD (Hình 4) là một hình chóp tứ giác đều.

Trong hình này.

- S gọi là đỉnh.

- Mặt ABCD là một hình vuông và được gọi là mặt đáy (gọi tắt là đáy)

- Các đoạn thẳng SA, SB, SC, SD bằng nhau và được gọi là các cạnh bên.

- Bốn mặt SAB, SBC, SCD, SDA là các tam giác cần đỉnh S bằng nhau và được gọi là bốn mặt bên.

- Các đoạn thẳng AB, BC, CD, DA được gọi là cạnh đáy.

- Gọi O là giao điểm hai đường chéo của mặt đáy, khi đó SO là đường cao, độ dài SO là chiều cao

Thực hành 2:

a) Hình chóp tứ giác đều A.MNPQ ở Hình 5 có:

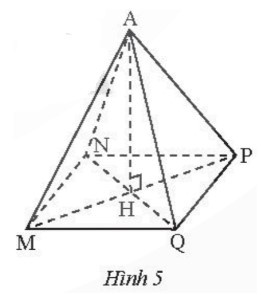
+ Đỉnh: A;

+ Các cạnh bên: AM, AN, AP, AQ;

+ Các mặt bên: AMN, ANP, APQ, AQM;

+ Các cạnh đáy: MN, NP, PQ, QM;

+ Mặt đáy: MNPQ;

+ Đường cao: AH.

b) Cho biết AM = 5 cm, MN = 4 cm. Tìm độ dài các cạnh AN, AP, AQ, NP, PQ, QM.

Xét hình chóp tứ giác đều A.MNPQ có:

+ AN = AP = AQ = AM = 5 cm;

+ NP = PQ = QM = MN = 4 cm.

Vận dụng 1.

a) Chiếc hộp dạng hình chóp tam giác đều S.MNP ở Hình 6 có:

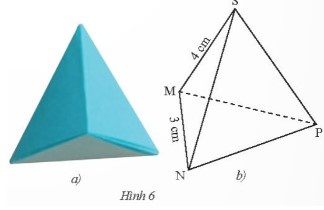
+ Mặt đáy: MNP;

+ Các mặt bên: SMN, SNP, SPM;

+ Các cạnh bên: SM, SN, SP.

b) Xét chiếc hộp dạng hình chóp tam giác đều S.MNP có:

+ SN = SP = SM =  4 cm;

+ NP = PQ = MN = 3 cm.

c) Tam giác đáy MNP là tam giác đều nên mỗi góc của tam giác này bằng 60°.

2. TẠO LẬP HÌNH CHÓP TAM GIÁC ĐỀU, HÌNH CHÓP TỨ GIÁC ĐỀU 

Thực hành 3.

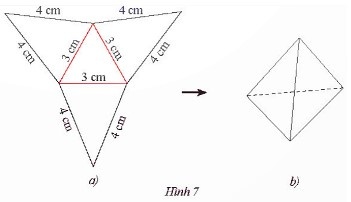
‒ Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.

+ Bước 1: Dùng thước thẳng và compa vẽ tam giác đều có cạnh 3 cm.

+ Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài tam giác vừa vẽ ở Bước 1 các tam giác cân có độ dài cạnh bên là 4 cm, với các cạnh đáy lần lượt là cạnh của tam giác đều đã vẽ ở Bước 1.

‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.

Vận dụng 2

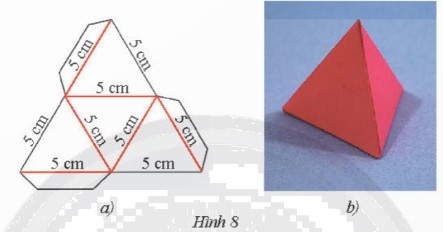
Cắt, gấp và dán hộp quà hình chóp tam giác đều có độ dài cạnh đáy và cạnh bên bằng 5 cm.

Gợi ý: Cắt theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.

+ Bước 1: Dùng thước thẳng và compa vẽ tam giác đều có cạnh 5 cm.

+ Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài tam giác vừa vẽ ở Bước 1 các tam giác đều có cạnh là 5 cm, có một cạnh là một trong ba cạnh của tam giác đều đã vẽ ở Bước 1.

+ Bước 3: Vẽ thêm một phần mép bìa để gấp (dán) các mép hộp như Hình 8a.

Thực hành 4. 

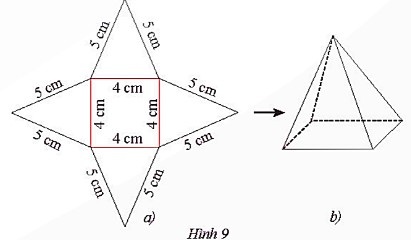
‒ Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a:

+ Bước 1: Dùng thước thẳng và êke vẽ hình vuông có cạnh 5 cm.

+ Bước 2: Dùng thước thẳng và compa vẽ ra phía ngoài hình vuông vừa vẽ ở Bước 1 các tam giác cân có cạnh bên là 5 cm, với các cạnh đáy lần lượt là một trong bốn cạnh của hình vuông đã vẽ ở Bước 1.

‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.

Vận dụng 3:

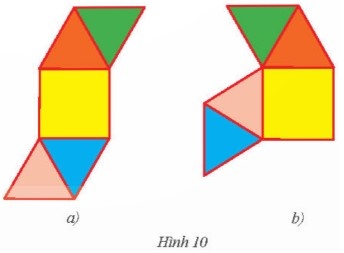
Tấm bìa Hình 10a có thể gấp thành hình chóp tứ giác đều.

Tấm bìa Hình 10b không thể gấp thành hình chóp tứ giác đều, vì khi gấp tạo lập hình chóp tứ giác đều thì tam giác màu xanh lá cây và tam giác màu hồng phải xếp chồng lên nhau, như vậy kết quả thiếu một mặt bên của hình chóp.