1. SỐ THẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN 

HĐ1:

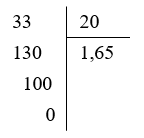
Lưu ý: Các số thập phân chỉ gồm hữu hạn chữ số khác 0 sau dấu "," được gọi là số thập phân hữu hạn. Chẳng hạn số 1,65 là số thập phân hữu hạn.

HĐ2:

Lưu ý: Phép chia ở HĐ2 không bao giờ chấm dứt. Nếu cứ tiếp tục chia thì trong phần thập phân của thương, chữ số 3 sẽ xuất hiện liên tiếp mãi. Ta nói rằng khi chia 4 cho 3 được số 1,333... .Số đó được gọi là số thập phân vô hạn tuần hoàn.

Nhận xét: Các số thập phân vô hạn tuần hoàn 1,333...; 0,2333...; 0,12313131... đã nêu ở trên có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.

4 : 3 = 1,333... = 1,(3)

7 : 30 = 0,2333... = 0,2(3)

1 219 : 9 900 = 0,12313131... = 0,12(31)

Luyện tập:

a) $\frac{1}{9}$ = 0,(1)

b) $\frac{-11}{45}$ = -0,2(4)

2. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ 

BTT:

a) 3 : 2 = 1,5;                                         37 : 25 = 1,48; 

    5 : 3 = 1,(6);                                       1 : 9 = 0,(1).

b) $\frac{3}{2}$ = 3 : 2 = 1,5;      

    $\frac{37}{25}$ = 37 : 25 = 1,48;      

    $\frac{5}{3}$ = 5 : 3 = 1,(6);      

    $\frac{1}{9}$ = 1 : 9 = 0,(1)

Nhận xét: Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ 3 (SGK - tr28)