Đề thi cuối kì 2 toán 10 KNTT: Đề tham khảo số 3
Trọn bộ Đề thi cuối kì 2 toán 10 KNTT: Đề tham khảo số 3 bộ sách mới Kết nối tri thức gồm nhiều câu hỏi ôn tập hay, các dạng bài tập phong phú giúp các em củng cố ôn luyện lại kiến thức thật tốt chuẩn bị tốt cho kì thi sắp tới. Tài liệu có kèm theo đáp án và lời giải chi tiết. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt điểm cao. Thầy cô và các em kéo xuống để tham khảo ôn luyện
PHÒNG GD&ĐT… TRƯỜNG THPT… | ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2022-2023 Thời gian làm bài: 90 phút |
I. TRẮC NGHIỆM (5 điểm – 25 câu)
- Cho hàm số
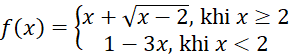 . Giá trị
. Giá trị 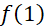 bằng
bằng
A. -2 B. 0 . C. không xác định. D. 2 . - Tập xác định của hàm số
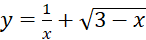 là
là
A.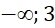 . B.
. B. 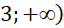 . C.
. C. 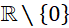 . D.
. D. 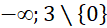 .
. 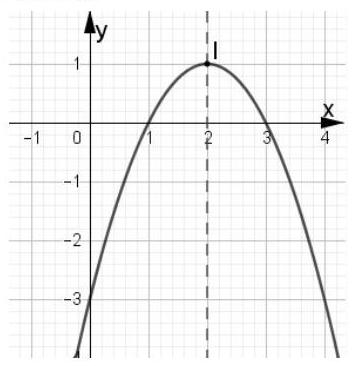 Hàm số nào có đồ thị như hình vẽ bên dưới?
Hàm số nào có đồ thị như hình vẽ bên dưới?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho tam thức bậc hai
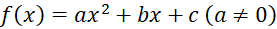 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A.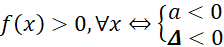 . B.
. B. 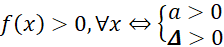 .
.
C.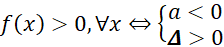 . D.
. D. 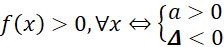 .
. Bảng xét dấu sau đây là của tam thức bậc 2 nào?
|
|
| - 0 + 0 - |
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Tam thức
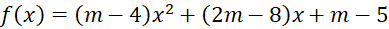 . không dương với mọi
. không dương với mọi  khi:
khi:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- Tập nghiệm của phương trình
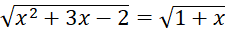 là
là
A. B.
B. 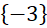 C.
C.  . D.
. D. .
. - Trong mặt phẳng tọa độ
 , viết phương trình đường thẳng đi qua điểm
, viết phương trình đường thẳng đi qua điểm 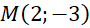 và có một vectơ pháp tuyến
và có một vectơ pháp tuyến 
A. . B.
. B.  .
.
C. . D.
. D.  .
. - Trong mặt phẳng tọa độ
 , cho hai đường thẳng
, cho hai đường thẳng  và
và  . Vị trí tương đối của hai đường thẳng
. Vị trí tương đối của hai đường thẳng  và
và  là
là
A.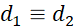 . B.
. B.  .
.
C. D. Cắt nhau và không vuông góc.
D. Cắt nhau và không vuông góc. - Trong mặt phẳng
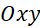 , gọi
, gọi 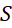 là tập hợp tất cả các giá trị của tham số
là tập hợp tất cả các giá trị của tham số 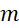 để góc giữa hai đường thẳng
để góc giữa hai đường thẳng 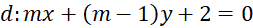 và
và 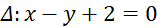 bằng
bằng  . Tích tất cả các phần tử của tập
. Tích tất cả các phần tử của tập 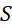 bằng
bằng
A. 1 . B.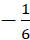 . C.
. C.  . D.
. D. 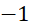 .
. - Tâm đường tròn
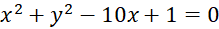 cách trục
cách trục 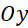 một khoảng bằng
một khoảng bằng
A. 5 . B. 0 . C. 10 . D.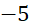 .
.
Tìm tất cả giá trị của tham số ![]() để phương trình
để phương trình ![]() là phương trình đường tròn và có bán kính nhỏ nhất.
là phương trình đường tròn và có bán kính nhỏ nhất.
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho Parapol
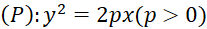 . Chọn mệnh đề đúng trong các mệnh đề sau:
. Chọn mệnh đề đúng trong các mệnh đề sau:
A.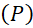 có tiêu điểm
có tiêu điểm 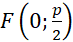 .
.
B. ![]() có tiêu điểm
có tiêu điểm ![]() .
.
C. ![]() có phương trình đường chuẩn
có phương trình đường chuẩn ![]() .
.
D. ![]() có phương trình đường chuẩn
có phương trình đường chuẩn ![]() .
.
- Một lớp có 23 học sinh nữ và 17 học sinh nam. Hỏi có bao nhiêu cách chọn một học sinh tham gia cuộc thi tìm hiểu môi trường?
A. 23 . B. 17 . C. 40 . D. 391 . - Trong một lớp học có 20 học sinh nam và 24 học sinh nữ. Giáo viên chủ nhiệm cần chọn 2 học sinh: 1 nam và 1 nữ tham gia đội cờ đỏ. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn?
A. 44 . B. 946 . C. 480 . D. 1892 . - Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5 !.7!. B.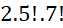 .
.
C.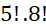 . D. 12 !.
. D. 12 !. - Cho đa giác đều
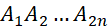 nội tiếp trong đường tròn tâm
nội tiếp trong đường tròn tâm 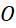 . Biết rằng số tam giác có đỉnh là 3 trong
. Biết rằng số tam giác có đỉnh là 3 trong 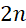 điểm
điểm 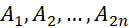 gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong
gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 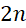 điểm
điểm 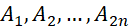 . Vậy giá trị của
. Vậy giá trị của 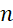 là:
là:
A.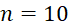 . B.
. B. 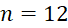 .
.
C.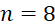 . D.
. D. 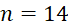 .
. - Cho khai triển
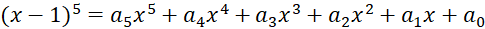 thì tổng
thì tổng 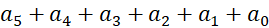 bằng:
bằng:
A.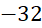 . B. 0 . C.1. D. 32 .
. B. 0 . C.1. D. 32 . - Số hạng có chứa
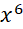 trong khai triển
trong khai triển 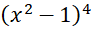 là:
là:
A.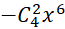 . B.
. B. 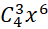 . C.
. C. 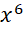 . D.
. D. 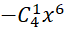 .
. - Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố
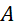 : "4 viên bi lấy ra có đúng hai viên bi màu trắng".
: "4 viên bi lấy ra có đúng hai viên bi màu trắng".
A.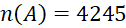 . B.
. B. 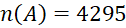 .
.
C.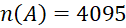 D.
D. 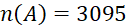
Từ các chữ số 1, 2, 3, 4 người ta lập được các số tự nhiên có ba chữ số đôi một khác nhau, tạo nên tập S. Lấy ngẫu nhiên hai chữ số từ tập S, số phần tử của không gian mẫu là:
A. 24 B. 276 C. 250 D. 252
- Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.
A.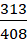 . B.
. B. 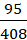 . C.
. C. 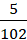 . D.
. D. 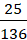 .
. - Một hộp có 10 phiếu, trong đó có 2 phiếu trúng thưởng. Có 10 người lần lượt lấy ngẫu nhiên mỗi người 1 phiếu. Tính xác suất người thứ ba lấy được phiếu trúng thưởng.
A. . B.
. B.  . C.
. C.  . D.
. D.  .
. - Tìm tất cả các giá trị thực của tham số
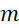 để bất phương trình
để bất phương trình 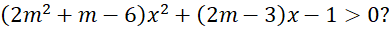
A.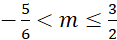 . B.
. B. 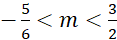 .
.
C.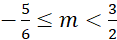 . D.
. D. 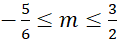 .
. Sắp xếp ngẫu nhiên 3 quyển sách Toán và 3 quyển sách Vật Lí lên một kệ dài. Xác suất để 2 quyển sách cùng một môn nằm cạnh nhau là:
A. . B.
. B. 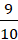 . C.
. C.  . D.
. D.  .
.II. TỰ LUẬN (3 điểm)
Câu 1. (1 điểm)
Một công ty bắt đầu sản xuất và bán một loại xe máy từ năm 2018. Số lượng loại xe máy đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 4 nghìn và 4,5 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ 2018 , số lượng xe máy loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm số bậc hai. Giả sử
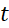 là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại xe máy đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm
là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại xe máy đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm 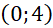 và
và 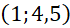 . Giả sử điểm
. Giả sử điểm 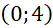 là đỉnh đồ thị của hàm số bậc hai này. Hỏi đến năm bao nhiêu thì số lượng xe máy đó bán được trong năm sẽ vượt mức 40 nghìn chiếc?
là đỉnh đồ thị của hàm số bậc hai này. Hỏi đến năm bao nhiêu thì số lượng xe máy đó bán được trong năm sẽ vượt mức 40 nghìn chiếc?Câu 2. (1 điểm)
Tìm tất cả các giá trị thực của tham số
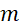 để bất phương trình sau có tập nghiệm là
để bất phương trình sau có tập nghiệm là 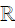 .
.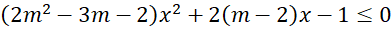
Câu 3. (1 điểm)
a) Viết phương trình đường thẳng
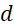 song song với
song song với 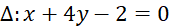 và cách điểm
và cách điểm 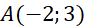 một khoảng bằng 3.
một khoảng bằng 3.b) Cho đường tròn
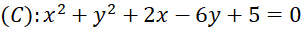 ; tiếp tuyến song song với đường thẳng
; tiếp tuyến song song với đường thẳng 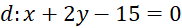 .
.Câu 4. (1 điểm)
Một nhóm học sinh gồm 5 nam và 5 nữ xếp thành một hàng ngang. Tính số cách sắp xếp để cho học sinh nam và học sinh nữ xen kẽ nhau.
Câu 5. (1 điểm)
Thầy giáo có 10 câu hỏi trắc nghiệm, trong đó có 6 câu đại số và 4 câu hình học. Thầy gọi bạn Nam lên trả bài bằng cách chọn lấy ngẫu nhiên 3 câu hỏi trong 10 câu hỏi trên để trả lời. Hỏi xác suất bạn Nam chọn ít nhất có một câu hình học là bằng bao nhiêu?
ĐÁP ÁN TRẮC NGHIỆM
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A D A D A A D D C C A D D C C C C B D C 21 22 23 24 25 B B C D B ĐÁP ÁN TỰ LUẬN
Câu 1.
Vì số lượng xe máy loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm số bậc hai nên gọi hàm số này có dạng
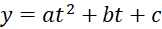 (trong đó
(trong đó 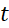 là thời gian (đơn vị năm),
là thời gian (đơn vị năm), 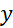 là số lượng xe máy bán được qua từng năm (đơn vị nghìn chiếc).
là số lượng xe máy bán được qua từng năm (đơn vị nghìn chiếc).
Điểm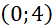 là đỉnh đồ thị của hàm số bậc hai, ta có
là đỉnh đồ thị của hàm số bậc hai, ta có 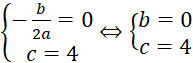 .
.
Đồ thị hàm số đi qua điểm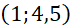 , ta có
, ta có 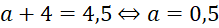 .
.
Hàm số cần tìm là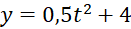 .
.
Để số lượng xe máy đó bán được vượt mức 40 nghìn chiếc thì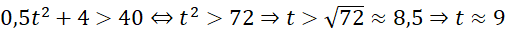 (năm).
(năm).
Vậy đến năm 2027 thì số lượng xe máy đó bán được vượt mức 40 nghìn chiếc.Câu 2.
Xét
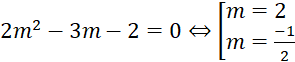
· Khi
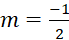 thì bất phương trình trở thành
thì bất phương trình trở thành 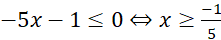 không nghiệm đúng với mọi
không nghiệm đúng với mọi 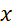
· Khi
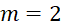 thì bất phương trình trở thành
thì bất phương trình trở thành 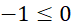 : nghiệm đúng với mọi
: nghiệm đúng với mọi 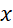
· Khi
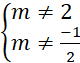 thì yêu cầu bài toán
thì yêu cầu bài toán 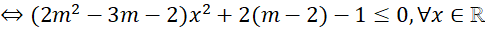
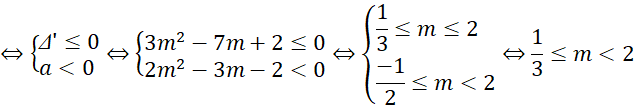
Kết hợp hai trường hợp ta được
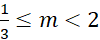 là giá trị cần tìm.
là giá trị cần tìm.Câu 3.
a) Ta có:
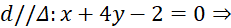 Phương trình
Phương trình 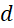 có dạng:
có dạng: 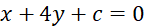 .
.
Mặt khác: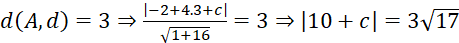
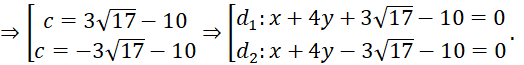
Vậy có hai đường thẳng thỏa mãn:
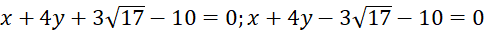 .
.
b)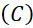 . có tâm
. có tâm 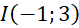 và bán kính
và bán kính 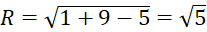 .
.
Tiếp tuyến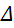 song song với
song song với 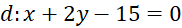 nên
nên 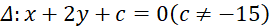 .
.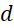 là tiếp tuyến của
là tiếp tuyến của 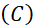 khi và chỉ khi:
khi và chỉ khi: 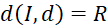
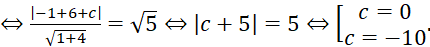
V có hai tiếp tuyến thỏa mãn đề bài: ![]() .
.
Câu 4.
Ta xếp 5 nam sinh trước tiên, số cách xếp là ![]() .
.
Giữa các nam sinh và hai đầu, cuối hàng sẽ có 6 vị trí (đánh số từ 1 đến 6 ) đề có thể sắp xếp 5 nữ sinh vào sao cho nam, nữ xen kẻ.
Trường họp 1: 5 nữ sinh xếp vào vị trí từ số 1 đến số 5 , số cách xếp là ![]() . Trường họ̣p
. Trường họ̣p ![]() nữ sinh xếp vào vị trí từ số 2 đến số 6 , số cách xếp là
nữ sinh xếp vào vị trí từ số 2 đến số 6 , số cách xếp là ![]() . Vậy số cách xếp hàng thỏa mãn đề bài là
. Vậy số cách xếp hàng thỏa mãn đề bài là ![]() .
.
Câu 5.
Chọn ngẫu nhiên 3 câu hỏi trong 10 câu hỏi thì số phần tử của không gian mẫu là ![]() .
.
Gọi ![]() : " Chọn được 3 câu và có ít nhất một câu hình học".
: " Chọn được 3 câu và có ít nhất một câu hình học".
Xét biến cố đối của ![]() là
là ![]() : " Chọn 3 câu mà không chọn được câu hình nào".
: " Chọn 3 câu mà không chọn được câu hình nào".
Ta có ![]() . Suy ra
. Suy ra ![]() .
.
CẤU TRÚC MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ I
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 25 câu
Câu hỏi tự luận: 5 câu
TT | Nội dung kiến | Đơn vị kiến thức | Mức độ nhận thức | Tổng | |||||||||
Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | Số CH | Điểm | ||||||||
TN | TL | TN | TL | TN | TL | TN | TL | TN | TL | ||||
1 | 1. Hàm số đồ thị và ứng dụng | 1.1. Hàm số, Hàm số bậc hai | 1 |
| 1 |
| 1 | 1 |
|
|
|
| TN: 1,6 điểm TL: 2 điểm |
1.2. Dấu của tam thức bậc hai | 1 |
| 1 |
| 1 | 1 | 1 |
| |||||
1.3. Phương trình quy về phương trình bậc hai |
|
| 1 |
|
|
|
|
| |||||
2 | 2. Phương pháp tọa độ trong mặt phẳng | 2.1. Phương trình đường thẳng. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách. | 1 |
| 1 | 0,5 |
1 |
|
|
|
|
| TN: 1,2 TL: 1 | |||
| 2.2. Đường tròn trong mặt phẳng tọa độ | 1 |
|
| 0.5 | 1 |
|
|
| ||||||||
| 2.3. Ba đường Conic | 1 |
|
|
|
|
|
|
| ||||||||
3 | 3. Đại số tổ hợp | 3.1. Quy tắc đếm | 1 |
| 1 | 1 |
|
|
|
|
|
| TN: 1,2 TL: 1
| |||
3.2. Hoán vị, chỉnh hợp và tổ hợp |
|
| 1 |
| 1 |
|
|
| ||||||||
|
| 3.3. Nhị thức Newton | 1 |
| 1 |
|
|
|
|
| ||||||
4 | 4. Tính xác suất theo định nghĩa cổ điển | Tính xác suất theo định nghĩa cổ điển | 2 |
| 2 | 1 | 1 |
|
|
|
|
| TN: 1 TL:1 | |||
| Tổng | 9 câu |
| 9 câu | 3 điểm | 6 câu | 2 điểm | 1 câu |
|
|
|
| |||||
| Tỉ lệ (%) |
| 18 | 48 | 32 | 2 |
|
| 100 | ||||||||
| Tỉ lệ chung (%) |
| 66 | 34 |
|
| 100 | ||||||||||
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA CUỐI HỌC KỲ 1
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
TT | Nội dung | Đơn vị | Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá | Số câu hỏi theo mức độ nhận thức | |||
Nhận | Thông | Vận | Vận dụng | ||||
1 | 1. Hàm số, đồ thị và ứng dụng | 1.1. Hàm số. Hàm số bậc hai | Nhận biết: – Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái niệm hàm số. – Nhận biết được các tính chất cơ bản của Parabola như đỉnh, trục đối xứng. Thông hiểu: – Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số. – Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. – Vẽ được Parabola (parabol) là đồ thị hàm số bậc hai. – Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị. Vận dụng: – Vận dụng được kiến thức của hàm số vào giải quyết bài toán thực tiễn (ví dụ: xây dựng hàm số bậc nhất trên những khoảng khác nhau để tính số tiền y (phải trả) theo số phút gọi x đối với một gói cước điện thoại,...). – Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn (ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabola,...). | 1 | 1 | 2 |
|
1.2. Dấu của tam thức bậc hai | Nhận biết: - Nhận biết, giải thích được định lí dấu của tam thức bậc hai Thông hiểu - Xét dấu của tam thức bậc hai. Vận dụng - Giải bất phương trình bậc hai. - Vận dụng giải quyết các vấn đề toán học. | 1 | 1 |
2
| 1 | ||
| 1.3. Phương trình quy về phương trình bậc hai | Nhận biết: - Nhận biết phương trình quy về phương trình bậc hai. Thông hiểu: - Giải một số phương trình chứa căn bậc hai đơn giản có thể quy về phương trình bậc hai. |
| 1 |
|
| |
2 | 2. Phương pháp tọa độ trong mặt phẳng | 2.1 Phương trình đường thẳng. Vị trí tương đối. Góc và khoảng cách | Nhận biết: - Nhận biết được vecto chỉ phương, vecto pháp tuyến, phương trình tổng quát, phương trình tham số của đường thẳng. - Nhận biết vị trí tương đối của hai đường thẳng. Thông hiểu: - Mô tả phương trình tổng quát, phương trình tham số của đường thẳng. - Giải thích mối liên hệ giữa đồ thị hàm bậc nhất và đường thẳng. - Lập phương trình đường thẳng. - Tính được góc giữa hai đường thẳng, khoảng cách từ một điểm đến một đường thẳng. Vận dụng: - Vận dụng vào một số bài toán liên quan đến phương trình đường thẳng, góc và khoảng cách. | 1 | 1,5 |
1
|
|
2.2. Đường tròn | Nhận biết: - Nhận biết phương trình đường tròn. Thông hiểu: - lập phương trình đường tròn. - Xác định tâm và bán kính. Vận dụng - Vận dụng kiến thức về phương trình đường tròn. | 1 | 0,5 |
1 |
| ||
2.3 Ba đường cônic | Nhận biết: - Nhận biết ba đường conic bằng hình học. - Nhận biết phương trình chính tắc của ba đường conic. Thông hiểu - Viết phương trình ba đường conic theo yêu cầu. Vận dụng - Giải quyết một số vấn đề toán học | 1 |
|
|
| ||
3 | 3. Đại số tổ hợp | 3.1. Quy tắc đếm | Nhận biết, thông hiểu: Nhận biết quy tắc đếm. Thông hiểu - Mô tả được quy tắc đếm, sơ đồ hình cây. Vận dụng: Vận dụng quy tắc cộng, quy tắc nhân để tính toán số cách thực hiện một công việc hoặc đếm số phần tử của một tập hợp. Vận dụng sơ đồ hình cây trong các bài toán đếm đơn giản.
| 1 | 2 |
|
|
3.2. Hoán vị, chỉnh hợp, tổ hợp. | Nhận biết - Nhận biết được hoán vị, chỉnh hợp, tổ hợp. Thông hiểu - Mô tả được về hoán vị, chỉnh hợp, tổ hợp. Vận dụng - Tính được số hoán vị, chỉnh hợp, tổ hợp. |
| 1 | 1 |
| ||
| 3.3. Nhị thức Newton | Thông hiểu: Biết cách khai triển nhị thức Newton bằng cách vận dụng tổ hợp trong trường hợp số mũ thấp. Vận dụng Vận dụng công thức khai triển nhị thức Newton để khai triển một số biểu thức đại số và ứng dụng trong ước lượng một số biểu thức số.
| 1 | 1 |
|
| |
4 | 4. Tính xác suất theo định nghĩa cổ điển | 4.1. Tính xác suất theo định nghĩa cổ điển
| Nhận biết: – Nhận biết được một số khái niệm gồm: Phép thử ngẫu nhiên, không gian mẫu, biến cố là tập con không gian mẫu, biến cố đối, định nghĩa cổ điển của xác suất, nguyên lí xác suất bé. Thông hiểu - Mô tả được không gian mẫu, biến cố trong một số phép thử đơn giản. - Mô tả được một tính chất cơ bản của xác suất. Vận dụng: - Tính xác suất trong một số bài toán đơn giản bằng phương pháp tổ hợp, sơ đồ hình cây. - Vận dụng được quy tắc tính xác suất của biến cố đối. | 2 | 3 | 1 |
|
Tổng | 9 | 12 | 8 | 1 | |||
Thêm kiến thức môn học
Đề thi Toán 10 Kết nối, trọn bộ đề thi Toán 10 Kết nối, Đề thi cuối kì 2 toán 10 KNTT:

Bình luận