Đề thi cuối kì 2 toán 10 KNTT: Đề tham khảo số 2
Trọn bộ Đề thi cuối kì 2 toán 10 KNTT: Đề tham khảo số 2 bộ sách mới Kết nối tri thức gồm nhiều câu hỏi ôn tập hay, các dạng bài tập phong phú giúp các em củng cố ôn luyện lại kiến thức thật tốt chuẩn bị tốt cho kì thi sắp tới. Tài liệu có kèm theo đáp án và lời giải chi tiết. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt điểm cao. Thầy cô và các em kéo xuống để tham khảo ôn luyện
PHÒNG GD&ĐT… TRƯỜNG THPT… | ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2022-2023 Thời gian làm bài: 90 phút |
I. TRẮC NGHIỆM (5 điểm – 25 câu)
Câu 1 :Tập xác định ![]() của hàm số
của hàm số ![]() là
là
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 2 : Cho hàm số ![]() . Tính
. Tính ![]() .
.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 3: Hàm số ![]() đồng biến trên khoảng nào trong các khoảng sau đây?
đồng biến trên khoảng nào trong các khoảng sau đây?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
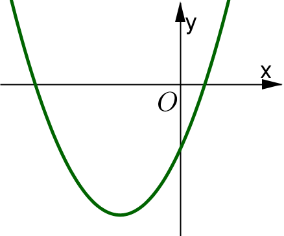
Câu 4 :Cho hàm số ![]() có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?
có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 5 :Tập nghiệm của bất phương trình ![]() là
là
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 6: Số nghiệm của phương trình ![]() là:
là:
A. Vô số B. 2
C. 1 D. 0
Câu 7 : Bất phương trình ![]() có tập nghiệm
có tập nghiệm ![]() là:
là:
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 8 : Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm ![]() và
và ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 10 : Góc giữa hai đường thẳng ![]() và
và ![]() là:
là:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 11 :Khoảng cách từ điểm M(5; -1) đến đường thẳng ![]() là:
là:
A. ![]() B.
B. ![]() C. 26 D.
C. 26 D. ![]()
Câu 12 :Xác định tâm và bán kính của đường tròn ![]()
A. Tâm ![]() bán kính
bán kính ![]() . B. Tâm
. B. Tâm ![]() bán kính
bán kính ![]() .
.
C. Tâm ![]() bán kính
bán kính ![]() . D. Tâm
. D. Tâm ![]() bán kính
bán kính ![]() .
.
Câu 13 : Phương trình đường tròn có tâm ![]() và bán kính
và bán kính ![]() là
là
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 14 :Cho đường hypebol có phương trình (H): ![]() . Tiêu cự của hypebol đó là:
. Tiêu cự của hypebol đó là:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 15: Trong mặt phẳng Oxy, đường tròn đi qua ba điểm ![]() có phương trình là:
có phương trình là:
A. | B. |
C. | D. |
Câu 16: Cho các số 1, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau:
A. 12 B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 17: Một liên đoàn bóng đá có ![]() đội, mỗi đội phải đá
đội, mỗi đội phải đá ![]() trận với mỗi đội khác,
trận với mỗi đội khác, ![]() trận ở sân nhà và
trận ở sân nhà và ![]() trận ở sân khách. Số trận đấu được sắp xếp là:
trận ở sân khách. Số trận đấu được sắp xếp là:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 18Có bao nhiêu cách sắp xếp ![]() nữ sinh,
nữ sinh, ![]() nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 19 :Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 20: Tìm tất cả giá trị của tham số ![]() để bất phương trình
để bất phương trình ![]() vô nghiệm:
vô nghiệm:
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 21:Tập nghiệm của bất phương trình ![]() là.
là.
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Câu 22 :Tổng ![]() bằng
bằng
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .
.
Câu 23: Cho 3 hộp, mỗi hộp đựng 5 cái thẻ được đánh số từ 1 đến 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Biến cố nào sau đây là biến cố chắc chắn?
A. X: “Tổng các số ghi trên ba tấm thẻ rút ra đều lớn hơn hoặc bằng 3”;
B. Y: “Tổng các số ghi trên ba tấm thẻ rút ra không nhỏ hơn 4”;
C. Z: “Tổng các số ghi trên ba tấm thẻ rút ra bằng 8”;
D. T: “Tổng các số ghi trên ba tấm thẻ luôn lớn hơn 15”.
Câu 24 :Có ba chiếc hộp. Mỗi hộp chứa 5 tấm thẻ được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp một thẻ rồi cộng các số trên 3 tấm thẻ vừa rút ra lại với nhau. Xác suất để kết quả thu được là số chẵn là:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 25: Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1; 3; 5; 7; 9. Xác suất để tìm được một số không có dạng ![]() là:
là:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
II. TỰ LUẬN (5 điểm)
Câu 1. (2 điểm)
a) Xét dấu của tam thức bậc hai: ![]() .
.
b) Với giá trị nào của ![]() thì phương trình
thì phương trình ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt ![]() thỏa mãn điều kiện
thỏa mãn điều kiện ![]() ?
?
Câu 2. (1 điểm)
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 1) và đường thẳng ![]()
a) Viết phương trình đường thẳng d qua A và vuông góc với đường thẳng ![]()
b) Viết phương trình đường tròn ![]() tâm A và tiếp xúc với đường thẳng
tâm A và tiếp xúc với đường thẳng ![]()
Câu 3. (1 điểm)
Hai hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả đen và 2 quả trắng, hộp thứ hai chứa 4 quả đen và 6 quả trắng.
a) Lấy ngẫu nhiên từ hộp thứ nhất 1 quả. Tính xác suất để lấy được 1 quả đen.
b) Lấy ngẫu nhiên từ mỗi hộp một quả. Tính xác suất để lấy được 2 quả cùng màu.
Câu 4. (1 điểm)
Có 5 bưu thiếp khác nhau và 6 bì thư khác nhau. Cần chọn 3 bưu thiếp bỏ vào 3 bì thư, mỗi bì thư một bưu thiếp và gửi cho 3 người bạn mỗi bạn một bưu thiếp. Hỏi có mấy cách thực hiện?
ĐÁP ÁN TRẮC NGHIỆM
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| D | A | C | D | C | C | D | B | D | A | A | A | A | B | C | B | A | B | D | D |
| 21 | 22 | 23 | 24 | 25 |
| C | D | A | D | C |
ĐÁP ÁN TỰ LUẬN
Câu 1.
a) ![]()
|
|
| + |
b) Xét phương trình ![]() có
có ![]()
Suy ra phương trình ![]()
Để phương trình (*) có hai nghiệm phân biệt ![]()
Khi đó, gọi ![]() là hai nghiệm của phương trình (*) suy ra
là hai nghiệm của phương trình (*) suy ra 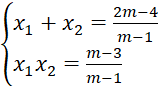
Theo bài ra, ta có ![]()
Kết hợp với (I) ta được ![]() là giá trị cần tìm.
là giá trị cần tìm.
Câu 2.
a) ![]() suy ra phương trình
suy ra phương trình ![]()
![]()
Phương trình ![]() .
.
b) ![]()
![]()
Phương trình đường tròn ![]() .
.
Câu 3.
a) ![]()
Gọi A là biến cố: “Lấy được một quả màu đen”.
Để lấy được một quả bóng đen từ hộp thứ nhất có: ![]()
Vì vậy xác suất để biến cố A xảy ra là:![]()
b) Ta có: ![]()
Gọi B là biến cố: “Lấy được 2 quả cùng màu”.
Các kết quả thuận lợi cho biến cố B được chia làm 2 phương án:
Phương án 1: Hai quả bóng lấy ra đều màu đen có ![]() cách.
cách.
Phương án 2: Hai quả bóng lấy ra đều màu trắng có ![]() cách.
cách.
![]()
Vậy xác suất của biến cố B là: ![]() .
.
Câu 4.
Cách để thực hiện được chia làm 3 công đoạn:
Công đoạn 1: Chọn 3 bưu thiếp có: ![]() cách.
cách.
Công đoạn 2: Ứng với 3 bưu thiếp số cách chọn 3 bì thư là: ![]() cách.
cách.
Công đoạn 3: Có 3! Cách để nhét 3 bưu thiếp vào mỗi phong bì tương ứng.
Vậy có:![]() cách.
cách.
CẤU TRÚC MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ I
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 25 câu
Câu hỏi tự luận: 4 câu
TT | Nội dung kiến | Đơn vị kiến thức | Mức độ nhận thức | Tổng | |||||||||
Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | Số CH | Điểm | ||||||||
TN | TL | TN | TL | TN | TL | TN | TL | TN | TL | ||||
1 | 1. Hàm số đồ thị và ứng dụng | 1.1. Hàm số, Hàm số bậc hai | 1 |
| 1 |
|
|
|
|
|
|
| TN: 1,6 TL: 2 điểm |
1.2. Dấu của tam thức bậc hai | 2 |
| 1 |
| 1 | 1 | 1 | 1 | |||||
1.3. Phương trình quy về phương trình bậc hai |
|
| 1 |
|
|
|
|
| |||||
2 | 2. Phương pháp tọa độ trong mặt phẳng | 2.1. Phương trình đường thẳng. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách. | 2 |
| 1 | 0,5 |
1 |
|
|
|
|
| TN: 1,8 TL: 1 |
| 2.2. Đường tròn trong mặt phẳng tọa độ | 1 |
| 2 | 0.5 | 1 |
|
|
| |||||
| 2.3. Ba đường Conic |
|
| 1 |
|
|
|
|
| |||||
3 | 3. Đại số tổ hợp | 3.1. Quy tắc đếm | 1 |
| 1 |
|
|
|
|
|
|
| TN: 1 TL: 1
|
3.2. Hoán vị, chỉnh hợp và tổ hợp |
|
| 1 | 1 | 1 |
|
|
| |||||
|
| 3.3. Nhị thức Newton |
|
| 1 |
|
|
|
|
| |||
4 | 4. Tính xác suất theo định nghĩa cổ điển | Tính xác suất theo định nghĩa cổ điển | 1 |
| 1 | 1 | 1 |
|
|
|
|
| TN: 0,6 TL:1 |
| Tổng | 8 câu |
| 11 câu | 3 điểm | 5 câu | 1 điểm | 1 câu | 1 điểm |
|
|
| ||
| Tỉ lệ (%) |
| 16 | 52 | 20 | 12 |
|
| 100 | |||||
| Tỉ lệ chung (%) |
| 68 | 32 |
|
| 100 | |||||||
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA CUỐI HỌC KỲ 1
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
TT | Nội dung | Đơn vị | Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá | Số câu hỏi theo mức độ nhận thức | |||
Nhận | Thông | Vận | Vận dụng | ||||
1 | 1. Hàm số, đồ thị và ứng dụng | 1.1. Hàm số. Hàm số bậc hai | Nhận biết: – Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái niệm hàm số. – Nhận biết được các tính chất cơ bản của Parabola như đỉnh, trục đối xứng. Thông hiểu: – Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số. – Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. – Vẽ được Parabola (parabol) là đồ thị hàm số bậc hai. – Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị.
Vận dụng: – Vận dụng được kiến thức của hàm số vào giải quyết bài toán thực tiễn (ví dụ: xây dựng hàm số bậc nhất trên những khoảng khác nhau để tính số tiền y (phải trả) theo số phút gọi x đối với một gói cước điện thoại,...). – Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn (ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabola,...). | 1 | 1 |
|
|
1.2. Dấu của tam thức bậc hai | Nhận biết: - Nhận biết, giải thích được định lí dấu của tam thức bậc hai Thông hiểu - Xét dấu của tam thức bậc hai. Vận dụng - Giải bất phương trình bậc hai. - Vận dụng giải quyết các vấn đề toán học. | 2 | 1 |
2 | 2 | ||
| 1.3. Phương trình quy về phương trình bậc hai | Nhận biết: - Nhận biết phương trình quy về phương trình bậc hai. Thông hiểu: - Giải một số phương trình chứa căn bậc hai đơn giản có thể quy về phương trình bậc hai. |
| 1 |
|
| |
2 | 2. Phương pháp tọa độ trong mặt phẳng | 2.1 Phương trình đường thẳng. Vị trí tương đối. Góc và khoảng cách | Nhận biết: - Nhận biết được vecto chỉ phương, vecto pháp tuyến, phương trình tổng quát, phương trình tham số của đường thẳng. - Nhận biết vị trí tương đối của hai đường thẳng. Thông hiểu: - Mô tả phương trình tổng quát, phương trình tham số của đường thẳng. - Giải thích mối liên hệ giữa đồ thị hàm bậc nhất và đường thẳng. - Lập phương trình đường thẳng. - Tính được góc giữa hai đường thẳng, khoảng cách từ một điểm đến một đường thẳng. Vận dụng: - Vận dụng vào một số bài toán liên quan đến phương trình đường thẳng, góc và khoảng cách. | 2 | 1,5 |
1 |
|
2.2. Đường tròn | Nhận biết: - Nhận biết phương trình đường tròn. Thông hiểu: - lập phương trình đường tròn. - Xác định tâm và bán kính. Vận dụng - Vận dụng kiến thức về phương trình đường tròn. | 1 | 2,5 |
1 |
| ||
2.3 Ba đường cônic | Nhận biết: - Nhận biết ba đường conic bằng hình học. - Nhận biết phương trình chính tắc của ba đường conic. Thông hiểu - Viết phương trình ba đường conic theo yêu cầu. Vận dụng - Giải quyết một số vấn đề toán học |
| 1 |
|
| ||
3 | 3. Đại số tổ hợp | 3.1. Quy tắc đếm | Nhận biết, thông hiểu: Nhận biết quy tắc đếm. Thông hiểu - Mô tả được quy tắc đếm, sơ đồ hình cây. Vận dụng: Vận dụng quy tắc cộng, quy tắc nhân để tính toán số cách thực hiện một công việc hoặc đếm số phần tử của một tập hợp. Vận dụng sơ đồ hình cây trong các bài toán đếm đơn giản. | 1 | 1 |
|
|
3.2. Hoán vị, chỉnh hợp, tổ hợp. | Nhận biết - Nhận biết được hoán vị, chỉnh hợp, tổ hợp. Thông hiểu - Mô tả được về hoán vị, chỉnh hợp, tổ hợp. Vận dụng - Tính được số hoán vị, chỉnh hợp, tổ hợp. |
| 1 | 2 |
| ||
| 3.3. Nhị thức Newton | Thông hiểu: Biết cách khai triển nhị thức Newton bằng cách vận dụng tổ hợp trong trường hợp số mũ thấp. Vận dụng Vận dụng công thức khai triển nhị thức Newton để khai triển một số biểu thức đại số và ứng dụng trong ước lượng một số biểu thức số.
|
| 1 |
|
| |
4 | 4. Tính xác suất theo định nghĩa cổ điển | 4.1. Tính xác suất theo định nghĩa cổ điển
| Nhận biết: – Nhận biết được một số khái niệm gồm: Phép thử ngẫu nhiên, không gian mẫu, biến cố là tập con không gian mẫu, biến cố đối, định nghĩa cổ điển của xác suất, nguyên lí xác suất bé. Thông hiểu - Mô tả được không gian mẫu, biến cố trong một số phép thử đơn giản. - Mô tả được tính chất cơ bản của xác suất. Vận dụng: - Tính xác suất trong một số bài toán đơn giản bằng phương pháp tổ hợp, sơ đồ hình cây. - Vận dụng được quy tắc tính xác suất của biến cố đối. | 1 | 2 | 1 |
|
Tổng | 8 | 14 | 6 | 2 | |||
Thêm kiến thức môn học
Đề thi Toán 10 Kết nối, trọn bộ đề thi Toán 10 Kết nối, Đề thi cuối kì 2 toán 10 KNTT:

Bình luận