ĐỀ THI GIỮA HỌC KỲ 1

MÔN: TOÁN 10 

I. TRẮC NGHIỆM (7 điểm)

Câu 1: Trong các bất đẳng phương trình dưới đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. 0x + 7y > 9 + 7y;

B. + y ≤ -10;

C. x² – 2y < 0;

D. x + 0.y² ≥ 5 – y.

Câu 2: Cho A = (-∞;5], B = (0; +∞). Tập hợp AB là 

A. [0; 5].

B. ;

C. (0; 5);

D. (0; 5].

Câu 3: Cho tam giác ABC có sinA = . Tính sin(B + C).

A. sin(B + C) = ;

B. sin(B + C) = ;

C. sin(B + C) = -;

D. sin(B + C) = - .

Câu 4: Tính giá trị biểu thức sau: M = sin75⁰ + tan45⁰ + cos165⁰.

A. M = 1;

B. M = 2;

C. M = 0;

D. M = -1.

Câu 5: Cho hình thoi ABCD có góc DAB = 60⁰ cạnh 2a. Gọi O là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai?

A.

B.

C.

D.

Câu 6: Cho tam giác ABC với M là trung điểm của BC. Mệnh đề nào sau đây đúng?

A.

B.

C.

D.

Câu 7: Cho hình bình hành ABCD, có AB = 4, BC = 5, BD = 7. Độ dài của AC gần nhất với giá trị nào sau đây:

A. 7,0; 

B. 5,9;

C. 5,7;

D. 7,5.

Câu 8: Cho hình bình hành ABCD. Mệnh đề nào sau đây là đúng?

A. ;

B. ;

C. ;
D. .

Câu 9: Cho tập M = và tập N = . Số các tập X có 4 phần tử thỏa mãn là:

A. 1;

B. 2;

C. 3;

D. 4.

Câu 10: Cho tam giác ABC có AB = 6, C = 45⁰, A = 80⁰. Độ dài cạnh BC là:

A. BC8,4;

B. BC4,3;

C. BC7,0;

D. BC5,2;

Câu 11: Gọi D là tập xác định của hàm số . Tìm tập hợp \D:

A. \D = [-2; +∞) \ ;

B. \D = (- ∞; - 2);

C. \D = (- ∞; -2) \ ;

D. \D = [- 2; + ∞) \ .

Câu 12: Trong các câu sau, câu nào không p-hải là mệnh đề?

A. Hôm nay trời mưa to quá!;

B. Hà Nội là thủ đô của nước Việt Nam;

C. là số vô tỉ;

D. 6 là số nguyên tố.

Câu 13:

A.

B.

C.

D.

Câu 14: Cho tam giác đều ABC có cạnh bằng 1. Giá trị bằng bao nhiêu? 

A.

B.

C.

D.

Câu 15: Cho A = , B = . Nhận xét nào dưới đây là đúng?

A. A B;

B. B A;

C. A = B;

D. Các đáp án A, B, C đều sai.

Câu 16: Miền nghiệm của hệ bất phương trình 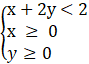là

A. miền trong tam giác OAB với A(2; 0), B(0; 1) và O(0; 0); 

B. miền trong tứ giác OMNP với O(0; 0), M(2; 0), N(0; 1) và P(-2; 2);

C. nửa mặt phẳng giới hạn bởi các đường thẳng Ox, Oy và đường thẳng x + 2y = 2;

D. nửa mặt phẳng bờ là đường thẳng x + 2y = 2 không chứa gốc tọa độ O(0; 0).

Câu 17: Với tam giác ABC có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là ba đỉnh của tam giác?

A. 6.

B. 4.

C. 5.

D. 3.

Câu 18: Các phần tử của tập hợp A = {: 2x² – 5x – 7 = 0} là:

A. A = .

B. A = .

C. A = .

D. A = .

Câu 19: Cho các điểm phân biệt A, B, C, D. Đẳng thức nào sau đây đúng?

A. .

B. .

C. .

D. .

Câu 20: Cho tam giác ABC có BC = 24, AC = 13, AB = 15. Nhận xét nào sau đây đúng về tam giác ABC.

A. ABC là tam giác tù, với A150⁰;

B. ABC là tam giác vuông tại A;

C. ABC là tam giác nhọn;

D. ABC là tam giác tù, với A118⁰.

Câu 21: Xét mệnh đề P: “: 2x – 3 ≥ 0”. Mệnh đề phủ định của mệnh đề P là

A. “: 2x – 3 ≥ 0”.

B. “: 2x – 3 < 0”.

C. “: 2x – 3 ≤ 0”.

D. “: 2x – 3 > 0”.

II. TỰ LUẬN (3 điểm)

Bài 1. (1 điểm)

a) Cho các tập hợp A = và B = . Tìm các tập hợp         AB, AB.

b) Tìm m để A = (m – 1; 2] là tập con của tập B = (0; m + 9).

Bài 2. (1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 5x - 10y  với cặp (x; y) thuộc vào miền nghiệm của hệ bất phương trình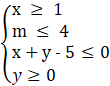        

Bài 3. (1 điểm)

a) (0,5 điểm) Cho tứ giác MNPQ. Gọi H, K lần lượt là trung điểm của MN và PQ. Chứng minh rằng .

b) (0,5 điểm) Cho hai điểm A, B. Tìm tập hợp điểm M thỏa mãn .

Đáp án

I. TRẮC NGHIỆM (7 điểm)

II. TỰ LUẬN (3 điểm)

Bài 1: (1 điểm)

a) Ta có: A B = .

A B = .

b) Để A là tập con của tâp B thì                                                      

Vậy với m > 1 thì tập A là tập con của tập B.

Bài 2. (1 điểm) 

+ Biểu diễn miền nghiệm 

Vẽ bốn đường thẳng:

d₁: x = 1, d₂: x = 4, d₃; x + y = 5; d₄: y = 0.

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.

Miền không gạch chéo (hay chính là miền trong của tứ giác OABC với O(0; 0), A(5; 0), B(4; 1), C(5; 0) và bao gồm cả các cạnh trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

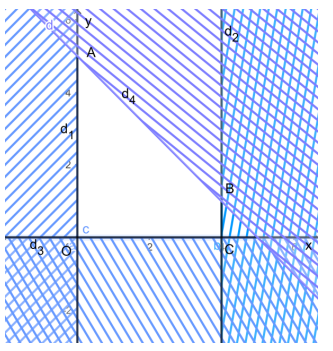
Ta chứng minh được giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F đạt được trên các đỉnh của tứ giác OABC. Khi đó ta có:

Tại O(0; 0): F(0; 0) = 5.0 – 10.0 = 0;

Tại A(0; 5): F(0; 5) = 5.0 – 10.5 = -50;

Tại B(4; 1): F(4; 1) = 5.4 – 10.1 = 10;

Tại C(5; 0): F(5; 0) = 5.5 – 10.0 = 25.

Vậy giá trị lớn nhất của F là 25 khi x = 5 và y = 0, giá trị nhỏ nhất của F là – 50 khi x = 0, y = 5.

Bài 3. (1 điểm)

a) Ta có: VT =

=

 = = = VP

b) Ta có:

Xác định H, K sao cho: và

+ Ta được

M nằm trên đường trung trực HK hoặc trung trực AB.