1. NHẬN BIẾT (7 câu)

Câu 1: Viết các biểu thức sau thành đa thức:

a) $(3x+1)^{2}$

b) $(4x+5y)^{2}$

c) $(5x-12)^{2}$

d) $(-x+2y^{2})^{2}$

Giải:

a) $(3x+1)^{2}=(3x)^{2}+2\times 3x\times 1+12=9x^{2}+6x+1$

b) $(4x+5y)^{2}=(4x)^{2}+2\times 4x\times 5y+(5y)^{2}=16^{2}+40xy+25y^{2}$

c) $(5x-12)^{2}=(5x)^{2}-2\times 5x\times12+(12)^{2}=25x^{2}-5x+14$

d) $(-x+2y^{2})^{2}=x^{2}-2\times x\times 2y^{2}+(2y^{2})^{2}=x^{2}-4xy^{2}+4y^{4}$

Câu 2: Viết các biểu thức sau thành đa thức:

a) $(4-x)(4+x)$

b) $(2y+7z)(2y-7z)$

c) $(x+2y^{2})(x-2y^{2})$

Giải:

a) $(4-x)(4+x)=4^{2}-x^{2}=16-x^{2}$

b) $(2y+7z)(2y-7z)=(2y)^{2}-(7z)^{2}=4y^{2}-49z^{2}$

c) $(x+2y^{2})(x-2y^{2})=x^{2}-(2y^{2})^{2}=x^{2}-4y^{4}$

Câu 3: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu

a) $a^{2}+10ab+25b^{2}$

b) $1+9a^{2}-6a$

c) $y^{2}+y+\frac{1}{4}$

d) $y^{2}+49-14y$

Giải:

a) $a^{2}+10ab+25b^{2}=a^{2}+2.a.5b+(5b)^{2}=(a+5b)^{2}$

b) $1+9a^{2}-6a=12-2.1.3a+(3a)^{2}=(1-3a)^{2}$

c) $y^{2}+y+\frac{1}{4}=y^{2}+2.y.\frac{1}{4}+(\frac{1}{4})^{2}=(y+\frac{1}{2})^{2}$

d) $y^{2}+49-14y=y^{2}-14y+49=y^{2}-2.y.7+7^{2}=(y-7)^{2}$

Câu 4: Viết các biểu thức sau thành đa thức:

a) $(3x+4)^{2}$

b) $(5x-y)^{2}$

c) $(xy-\frac{1}{2}y)^{2}$

Giải:

a) $(3x+4)^{2}= 9x^{2}+24x+16$

b) $(5x-y)^{2}=25x^{2}-10xy+y^{2}$

c) $(xy-\frac{1}{2}y)^{2}$$=x^{2}y^{2}-xy^{2}+\frac{1}{4}y^{2}$

Câu 5. Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu

a) $x^{2}+2x+1$

b) $9-24x+16x^{2}$

c) $4x^{2}+\frac{1}{4}+2x$

Giải:

a) $x^{2}+2x+1=x^{2}+2x+1^{2}=(x+1)^{2}$

b) $9-24x+16x^{2}=32-24x+(4x)2=(3-4x)^{2}$

c) $4x^{2}+\frac{1}{4}+2x=(2x)^{2}+2x+(\frac{1}{2})^{2}=(2x+\frac{1}{2})^{2}$

Câu 6. Viết các biểu thức sau thành đa thức:

a) $(3x-5)(3x+5)$

b) $(x-2y)(x+2y)$

c) $(-x-\frac{1}{2}y)(-x+\frac{1}{2}y)$

Giải:

a) $(3x-5)(3x+5)=(3x)^{2}-5^{2}=9x^{2}-25$

b) $(x-2y)(x+2y)=x^{2}-(2y)^{2}=x^{2}-4y^{2}$

c) $(-x-\frac{1}{2}y)(-x+\frac{1}{2}y)=(-x)^{2}-(\frac{1}{2}y)^{2}=x^{2}-\frac{1}{4}y^{2}$

Câu 7. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) $4x^{2}+28x+49$

b) $4a^{2}+20ab+25b^{2}$

c) $16^{2}-8y+1$

d) $9x^{2}-6xy+y^{2}$

Giải:

a) $4x^{2}+28x+49=(2x)^{2}+2.2x.7+72=(2x+7)^{2}$

b) $4a^{2}+20ab+25b^{2}=(2a)^{2}+2.2a.5b+(5b)^{2}=(2a+5b)^{2}$

c) $16^{2}-8y+1=(4y)^{2}-2.4y.1+1^{2}=(4y-1)^{2}$

d) $9x^{2}-6xy+y^{2}=(3x)^{2}-2.3x.y+y^{2}=(3x-y)^{2}$

2. THÔNG HIỂU (6 câu)

Câu 1. Tính nhanh

a) $52^{2}$

b) $98^{2}$

c) $49^{2}$

Giải:

a) $52^{2}=(50+2)^{2}=50^{2}+2\times 50\times 2+2^{2}=2500+200+4=2704$

b) $98^{2}=(100-2)^{2}=100^{2}-2\times 100\times 2+2^{2}=10000-400+4=9604$

c) $49^{2}=(50-1)^{2}=50^{2}-2\times 50\times 1+1^{2}=2500-100+1=2401$

Câu 2. Tính nhanh

a) 48.52

b) 82.78

c) 87.93

d) $125^{2}-25^{2}$

Giải:

a) 48.52=(50-2)(50+2)=$50^{2}-2^{2}=2500-4=2496$

b) 82.78=(80+2)(80-2)=$80^{2}-2^{2}=6400-4=6396$

c) 87.93=(90-3)(90+3)=$90^{2}-3^{2}=8100-9=8091$

d) $125^{2}-25^{2}$=(125-25)(125+25)=100.150=15000

Câu 3: Viết các biểu thức sau thành đa thức:

a) $(a-1)(a+1)(a^{2}+1)$

b) $(xy+1)^{2}-(xy-1)^{2}$

Giải:

a) $(a-1)(a+1)(a^{2}+1)=(a^{2}-1)(a^{2}+1)=(a^{2})^{2}-1=a^{4}-1$

b) $(xy+1)^{2}-(xy-1)^{2}=(xy+1-xy+1)(xy+1+xy-1)=2(2xy)=4xy$

Câu 4: Tính nhanh

a) $38\times 42$

b) $102^{2}$

c) $198^{2}$

d) $75^{2}-25^{2}$

Giải:

a) $38\times 42$=$(40-2)(40+2)=40^{2}-2^{2}+1600-4=1598$

b) $102^{2}$=$(100+2)^{2}=100^{2}+2\times 100\times 2+2^{2}=10000+400+4=10404$

c) $198^{2}$=$(200-2)^{2}=200^{2}-2\times 200\times 2+2^{2}=40000-800+4=39204$

d) $75^{2}-25^{2}$=$(75-25)(75+25)=50\times 100=5000$

Câu 5: Tính giá trị của biểu thức: $A=x^{2}+6x+10$ tại x =-103

Giải:

$A=x^{2}+6x+10=x^{2}+2.x.3+3^{2}+1=(x+3)^{2}+1$

Tại x = -103 thì $A=(x+3)^{2}+1=(-103+3)^{2}+1=(-100)^{2}+1=10001$

Câu 6. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x:

$C=(3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

Giải:

$C=(3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

$=(3x-1)^{2}+(3x+1)^{2}-2(3x-1)(3x+1)$

$=(3x-1)^{2}-2(3x-1)(3x+1)+(3x+1)^{2}$

$=(3x-1-3x-1)^{2}$

$=(-2)^{2}$

=4

Giá trị của biểu thức C luôn luôn bằng 4 với mọi x

3. VẬN DỤNG (5 câu)

Câu 1: 

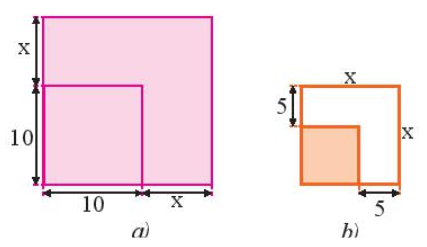
a) Một mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.

b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh 5 m thì được một mảnh vườn hình vuông với cạnh là x (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.

Giải: 

a) Biểu thức biểu thị diện tích mảnh vườn sau khi mở rộng: 

$(x+10)^{2}=x^{2}+20x+100$

b) Biểu thức biểu thị diện tích mảnh vườn trước khi mở rộng: 

$(x-5)^{2}=x^{2}-10x+25$

Câu 2:

Em hãy giúp các bạn Lan, Mai, Nam giải đáp câu hỏi.

Giải:

$65^{2}-35^{2}=(65-35)(65+35)=30.100=3000$

$102.98=(100+2)(100-2)=100^{2}-22=10000-4=9996$

Câu 3. 

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 dưới dạng đa thức

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x - 2 dưới dạng đa thức

Giải:

$a) (2x+3)^{2}=4x^{2}+12x+9$

$b) (3x-2)^{3}=27x^{3}-54x^{2}+36x-8$

Bài 4. Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu chiều dài và chiều rộng tăng thêm a cm?

Giải:

Thể tích hình hộp chữ nhật ban đầu là: $5^{3}=125(cm^{3})$

Thể tích hình hộp chữ nhật khi chiều dài và chiều rộng tăng thêm a cm là: $5(5+a)^{2}=5(25+10a+a^{2})=125+50+5a^{2} (cm^{3})$

Khi đó thể tích hình chữ nhật sẽ tăng thêm $125+50a+5a^{2}-125=50+5a^{2} (cm^{3})$

Câu 5. 

a) Cho x + y = 12 và xy = 35. Tính $(x-y)^{2}$

b) Cho x - y = 8 và xy = 20. Tính $(x+y)^{2}$

Giải:

a) $(x-y)^{2}=x^{2}-2xy+y^{2}=(x^{2}+2xy+y^{2})-4xy=(x+y)^{2}-4xy=12^{2}-4\times 35=4$

b) $(x+y)^{2}=x^{2}+2xy+y^{2}=(x^{2}-2xy+y^{2})+4xy=(x-y)^{2}+4xy=8^{2}+4\times 20=144$

4. VẬN DỤNG CAO (4 câu)

Câu 1: Cho biểu thức: $A=(2x-3)^{2}-(x+1)(x+5)+2$

Rút gọn và tìm giá trị nhỏ nhất của  A.

Giải:

$A=(2x-3)^{2}-(x+1)(x+5)+2$

$=3x^{2}-18x+6$

$=3.(x^{2}-6x+2)$

$=3.(x-3)^{2}-21$

GTNN của A = 21 khi x =  3

Câu 2. Tìm giá trị lớn nhất của biểu thức:

 $A=-2x^{2}-10y^{2}+4xy+4x+4y+2023$

Giải:

$A=-2x^{2}-10y^{2}+4xy+4x+4y+2022$

$=-2\left [ x^{2}-2x(y+1)+(y+1)^{2}+(4y^{2}-4y+1)-1013 \right ]$

$=-2(x-y-1)^{2}-2(2y-1)^{2}+2026$   

GTLN của A bằng 2026 khi $y=\frac{1}{2};x=\frac{3}{2}$

Câu 3. Cho x + y = 8. Tìm giá trị nhỏ nhất của biếu thức $A=x^{2}+y^{2}$

Giải:

Ta có $x^{2}+1\geq 2x,y^{2}+1\geq 2y$

Nên $x^{2}+y^{2}+2\geq 2(x+y)$

$\Rightarrow x^{2}+y^{2}\geq 2(x+y)-2$

$\Rightarrow x^{2}+y^{2}\geq 2.8-2$

$\Rightarrow x^{2}+y^{2}\geq 14$

Vậy $A_{min}=x^{2}+y^{2}=14$

Câu 4. Chứng minh rằng $a^{n}-b^{n}= (a +b)(a^{n-1}-b^{n-1}) - ab(a^{n-2}-b^{n-2})$, với n là số tự nhiên và n>1

Giải:

Với n là số tự nhiên và n>1, ta có:

$a^{n}-b^{n}= (a +b)(a^{n-1}-b^{n-1}) - ab(a^{n-2}-b^{n-2})$

$=a^{n}-ab^{n-1}+a^{n-1}b-b^{n}-a^{n-1}b+ab^{n-1}$

$=a^{n}-b^{n}$