Slide bài giảng toán 7 kết nối bài Luyện tập chung trang 82 (2 tiết)

Slide điện tử bài Luyện tập chung trang 82 (2 tiết). Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 7 kết nối tri thức sẽ khác biệt

Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu

Tóm lược nội dung

LUYỆN TẬP CHUNG

Bài tập 9.31: Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

Trả lời rút gọn:

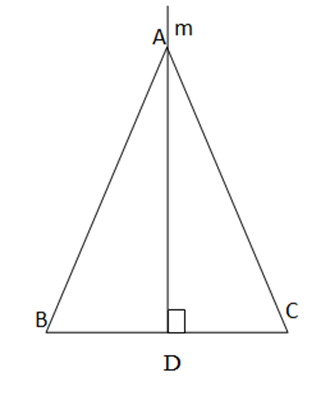
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC

=> AD là đường trung tuyến của BC

Ta có ∆ ADB và ∆ ADC đều vuông tại D

Xét ∆ ADB và ∆ ADC , ta có

AD chung

DB = DC ( D là trung điểm của BC)

∆ ADB và ∆ ADC đều vuông tại D

=> ∆ ADB = ∆ ADC

=> AB= AC

=> ∆ABC cân tại A

Bài tập 9.32: Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Trả lời rút gọn:

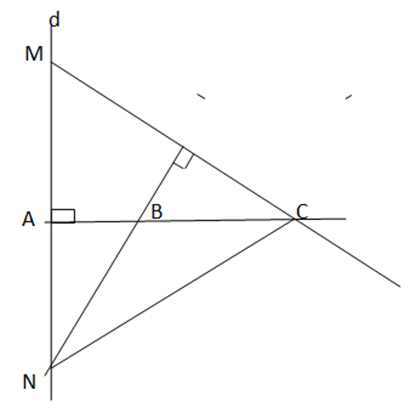
Ta có: BN ⊥ CM, CA ⊥ MN. CA và BN cắt nhau tại B

=> B là trực tâm của ∆ MNC

=> MB ⊥ CN

Bài tập 9.33: Có một mảnh tôn hình tròn cần đục một lỗ ở tâm. Lam the nao đe xác định được tâm của mảnh tôn đó?

Trả lời rút gọn:

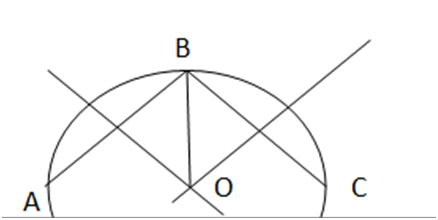
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.

- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D. Khi đó D là tâm cần xác định.

Bài tập 9.34: Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC.Chứng minh rằng nếu đường thắng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Trả lời rút gọn: