Slide bài giảng toán 7 kết nối bài 14: Trường hợp bằng nhau thứ 2 và thứ 3 của tam giác (2 tiết)

Tóm lược nội dung

BÀI 14. TRƯỜNG HỢP BẰNG NHAU THỨ HAI VÀ THỨ BA CỦA TAM GIÁC

1. TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC

Bài 1: Vẽ = . Lấy điểm B trên tia Ax và điểm C trên tia Ay  sao cho AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC . Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC

Trả lời rút gọn:

Bài 2: Vẽ thêm tam giác A’B’B với = , A’B’ = 4 cm và A’C’ = 3 cm. Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài cạnh tương ứng của hai tam giác ABC và A’B’C’

• Hai tam giác ABC và A’B’C’ có bằng nhau không?
• Độ dài các cạnh BC và B’C’ của hai tam giác các bạn khác vẽ không
• Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không

Trả lời rút gọn:

- Các cạnh tương ứng của hai tam giác ABC và A’B’C’ bằng nhau.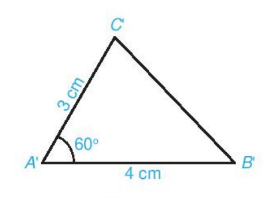

- Hai tam giác ABC và A’ B’ C’ bằng nhau theo trường hợp cạnh – cạnh – cạnh.

- Các tam giác vẽ được đều bằng nhau.

Bài 3: Trong Hình 4.29, hai tam giác nào bằng nhau

Trả lời rút gọn:

+ Xét hai tam giác ABC và MNP có:

AB = MN

AC = MP

Hoặc .

Bài 4: Hai tam giác ABC và MNP trong hình 4.31 có bằng nhau không? Vì sao

Trả lời rút gọn:

+) Xét tam giác MNP có:

.

+ Xét hai tam giác ABC và MNP có:

AB = MN

AC = MP;

(c.g.c)

Bài 5: Cho Hình 4.32 biết = , OA = OD và AB = CD. Chứng minh rằng

1. AC = DB
2. 

Trả lời rút gọn:

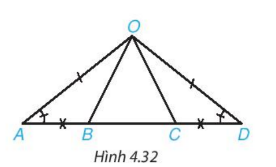
a) AC = AB + BC = DC + BC = DB

b) Xét hai tam giác OAC và ODB có:

AO = DO;

AC = DB (chứng minh trên)

(c.g.c)

2. TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC (GÓC - CẠNH - GÓC)

Bài 1: Vẽ đoạn thẳng BC=3cm. Vẽ tia Bx và Cy sao cho = ,

= như hình 4.33. Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC. Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC

Trả lời rút gọn:

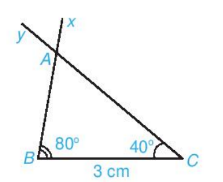
Bài 2: Vẽ thêm tam giác A′B′C′ sao cho B’C’ = 3 cm, = ,  = . Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạn của hai tam giác ABC và A’B’C’. Hai tam giác ABC và A’B’C’ có bằng nhau không?

Trả lời rút gọn:

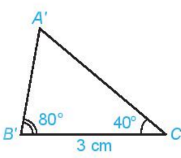
- Các cạnh tương ứng của hai tam giác ABC và A’B’C’ bằng nhau.

- Hai tam giác ABC và A’B’ C’ bằng nhau theo trường hợp cạnh – cạnh – cạnh.

- Các tam giác HS vừa vẽ đều bằng nhau.

Bài 3: Hai tam giác nào trong Hình 4.35 bằng nhau

Trả lời rút gọn:

+ Xét hai tam giác ABC và MNP có:

BC = PN

Bài 4: Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau

Trả lời rút gọn:

Xét 2 tam giác ABD và CBD ta có :

• =
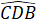
• BD chung
• =

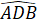=> ΔABD = ΔCBD

Bài 5: Bạn Lan nói rằng “ Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng  bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau. Theo em bạn Lan nói có đúng không? Vì sao

Trả lời rút gọn:

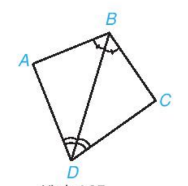
Xét tam giác ABD và CBD có:

BD chung

(g.c.g)

Thử thách nhỏ:

Xét tam giác ABC và A’B’C’ có:

AC = A’C’

(g.c.g)

Bạn Lan nói đúng.

BÀI TẬP CUỐI SGK

Bài 4.12: Trong mỗi hình bên (H.4.39) hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau

Trả lời rút gọn:

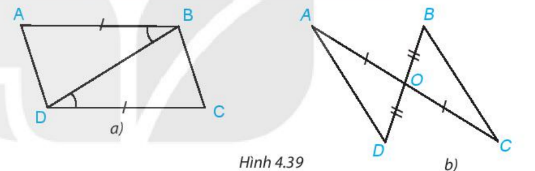
(c.g.c) vì: 

(giả thiết), là cạnh chung.

(c.g.c) vì;

(giả thiết), (hai góc đối đỉnh), (giả thiết).

Bài 4.13: Cho hai đoạn thẳng AC và BD cắt nhau tại điẻm O sao cho OA = OC, OB = OD như hình 4.40

1. Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau
2. Chứng minh rằng và

Trả lời rút gọn:

a) (c.g.c), (c.g.c).

b) và có:

(vì là cạnh chung, (vì .

Do đó (g.c.g).

Bài 4.14: Chứng minh rằng hai tam giác ADE và BCE trong hình 4.41 bằng nhau

Trả lời rút gọn:

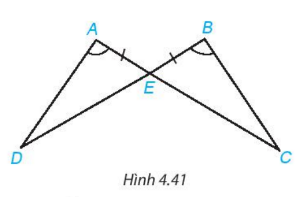
và có:

(theo giả thiết), (hai góc đối đỉnh).

Do đó (g.c.g).

Bài 4.15: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh

1. và
2. 

Trả lời rút gọn:

a) và có: 

(hai góc so le trong), (theo giả thiết), (hai góc so le trong).

 Do đó (g.c.g). 

b) và có:

  (hai góc so le trong), , (hai góc đối đỉnh). 

Do đó g.c.g), suy ra