Slide bài giảng toán 7 kết nối bài 32: Quan hệ giữa đường vuông góc và đường xiên

Tóm lược nội dung

BÀI 32. QUAN HỆ ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN

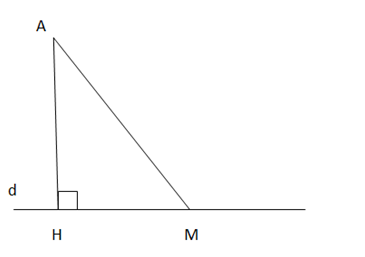
Bài 1: Cho điểm A không nằm trên đường thẳng d.

a) Hãy vẽ đường vuông góc AH và một đường xiên

AM từ A đến d.

b) Em hãy giải thích vì sao AH < AM.

Trả lời rút gọn:

a)

b) Xét tam giác AHM vuông tại H có: 

cạnh huyền AM là cạnh lớn nhất của tam giác.

AH < AM

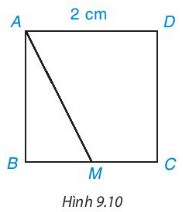
Bài 2: Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

b) So sánh hai đoạn thẳng AB và AM.

c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

Trả lời rút gọn:

a)Đường vuông góc: AB

   Đường xiên: AM

b) Theo định lí đường vuông góc và đường xiên, ta thấy AB là đường vuông góc kẻ từ A đến BC nên AB sẽ ngắn nhất. AB < AM.

c) Ta có CB ⊥ AB

CB là khoảng cách từ điểm C đến AB

Vì ABCD là hình vuông 

CB = AD = 2cm

Vậy khoảng cách từ C đến AB là 2 cm.

Bài 3: a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức la neu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.

b) Xét hình vuông ABCD và một điểm M tuỳ ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?

Trả lời rút gọn:

a) Xét tam giác AMN có: 

M là góc tù 

AN là cạnh lớn nhất AM < AN

b) + Khi M thay đổi trên một cạnh mút A của hình vuông ABCD thì độ dài AM không lớn hơn độ dài một cạnh của hình vuông. 

+ Khi M thay đổi trên một cạnh mút C thì AM không lớn hơn AC.

M C thì độ dài AM bằng độ dài AC là lớn nhất.

BÀI TẬP CUỐI SGK

Bài 9.6: Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?

Trả lời rút gọn:

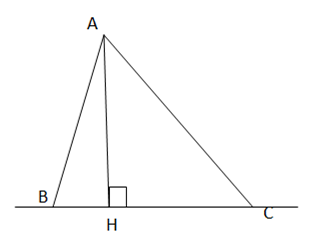
Có: AH ⊥ BC và AH là đoạn ngắn nhất so với đường xiên AB và đường xiên AC

AH chính là khoảng cách từ a đến đoạn thẳng BC

Bài 9.7: Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông

a) Đỉnh nào cách đều hai điểm A và C?

b) Đỉnh nào cách đều hai đường thẳng AB và AD?

Trả lời rút gọn:

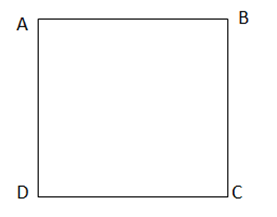
a) Hai đỉnh B và D cách đều hai điểm A và C.

b) Hai đỉnh C, A cách đều hai đường thẳng AB và AD

Bài 9.8: Cho tam giác cân ABC, AB = AC. Lấy điểm M tuỳ ý nằm giữa B và C (H.9.12).

a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM

nhỏ nhất.

b) Chứng minh rằng với mọi điểm M thì AM < AB.

Trả lời rút gọn:

a)

Gọi M₁ là trung điểm của cạnh đáy BC. Suy ra AM₁ ⊥ BC  (Vì tam giác ABC cân tại A). 

AM₁ chính là khoảng cách từ A đến BC.

Theo định lí về đường xiên và đường vuông góc ta có: AM AM₁

AM₁ nhỏ nhất AM AM₁ hay M M₁

Vậy khi M là trung điểm của BC thì AM sẽ có độ dài nhỏ nhất

b) C1:

Tam giác ABC cân tại A, M nằm giữa B và C Cần chứng minh AM < AB = AC.

+ Nếu thì theo định lí đường vuông góc và đường xiên, ta có: 

AM < AB

+ Nếu là góc tù là góc lớn nhất trong tam giác ABC AB > AM.

+ Nếu là góc nhọn là góc tù (vì kề bù với ).

Xét tam giác AMC có: 

là góc lớn nhất AC > AM.

C2: Khi M nằm giữa C và B

+ Nếu BM < MC là góc tù.

Theo định lý về góc và cạnh đối diện có: AB > AM

+ Nếu BM > MC là góc tù. 

Theo định lý về góc và cạnh đối diện có: AC > AM

Mà AB=AC 

AB > AM

Vậy với mọi điểm M thì AM < AB.

Bài 9.9: Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.(Gợi ý. So sánh MN với NB, NB với BC).

Trả lời rút gọn:

Nối N với B

Xét vuông tại A có:

là góc nhọn

180^o - là góc tù.

Xét có:

lớn nhất MN < BN (1)

Tương tự ta có:

Xét vuông tại A có:

là góc nhọn

là góc tù.

Xét có:

lớn nhất BN < BC (2)

Từ (1) và (2) MN < BC.